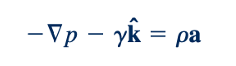Persamaan Dasar Bidang Tekanan
Meskipun kita telah menjawab pertanyaan tentang bagaimana tekanan pada suatu titik bervariasi dengan arah, sekarang kita dihadapkan pada pertanyaan yang sama pentingnya—bagaimana tekanan dalam fluida di mana tidak ada gaya geser bervariasi dari titik ke titik? Untuk menjawab pertanyaan ini, pertimbangkan sebuah elemen fluida berbentuk persegi kecil yang diambil dari posisi sembarang dalam massa fluida yang ingin kita amati seperti yang diilustrasikan dalam Gambar 2.2. Ada dua jenis gaya yang bekerja pada elemen ini: gaya permukaan akibat tekanan dan gaya benda yang sama dengan berat elemen. Jenis gaya benda lain yang mungkin, seperti yang disebabkan oleh medan magnet, tidak akan dipertimbangkan dalam teks ini.
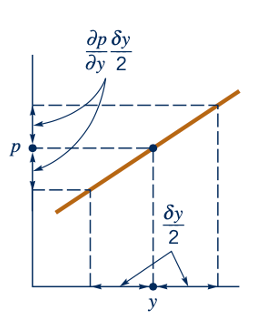
Jika kita membiarkan tekanan di pusat elemen ditetapkan sebagai p, maka tekanan rata-rata pada berbagai permukaan dapat dinyatakan dalam hal p dan turunannya, seperti yang ditunjukkan dalam Gambar 2.2. Kita sebenarnya menggunakan ekspansi deret Taylor dari tekanan di pusat elemen untuk mendekati tekanan pada jarak pendek dan mengabaikan suku-suku orde yang lebih tinggi yang akan menghilang saat kita membiarkan dx, dy, dan dz mendekati nol. Ini diilustrasikan oleh gambar di margin. Untuk kesederhanaan, gaya permukaan dalam arah x tidak ditunjukkan. Gaya permukaan resultant dalam arah y adalah
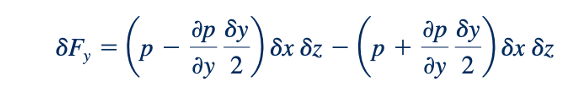
Atau
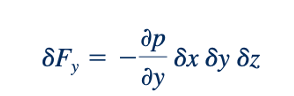
Demikian pula, untuk arah x dan z, gaya permukaan resultant adalah
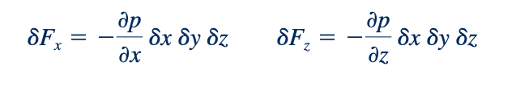
Gaya permukaan resultant yang bekerja pada elemen dapat dinyatakan dalam bentuk vektor sebagai
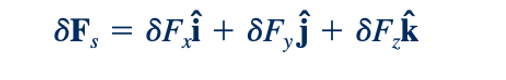

Atau
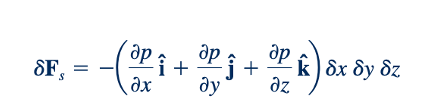
di mana i, j , dan k adalah vektor satuan sepanjang sumbu koordinat yang ditunjukkan dalam Gambar 2.2. Kelompok suku dalam tanda kurung dalam Persamaan 2.1 mewakili gradien tekanan dalam bentuk vektor dan dapat ditulis sebagai

Dimana
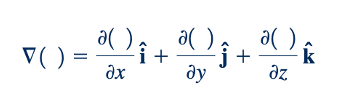
dan simbol ∇ adalah operator vektor gradien atau "del". Dengan demikian, gaya permukaan resultant per unit volume dapat dinyatakan sebagai

Karena sumbu z adalah vertikal, berat elemen tersebut adalah

Di mana tanda negatif menunjukkan bahwa gaya yang disebabkan oleh beratnya bergerak ke bawah ke arah negatif sumbu z. Hukum kedua Newton, yang diterapkan pada elemen fluida, dapat dinyatakan sebagai
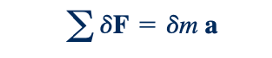
di mana ∑𝛿𝐹 mewakili gaya resultant yang bekerja pada elemen, a adalah percepatan elemen, dan 𝛿m adalah massa elemen, yang dapat dituliskan sebagai ρ, 𝛿x 𝛿y 𝛿z, di mana ρ adalah massa jenis fluida. Dengan demikian,
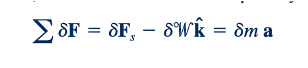
Atau
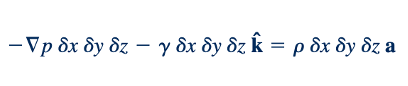
dan, oleh karena itu,