Persamaan Koreksi Tekanan
Derivasi yang disajikan selanjutnya didasarkan pada karya Patankar dan Spalding [2, 3], yang mengembangkan implementasi awal algoritma SIMPLE (Semi Implicit Method for Pressure Linked Equations).
Dimulai dengan persamaan kontinuitas dan momentum yang diberikan masing-masing oleh (Gambar 15.3)

solusi dilanjutkan dengan memberikan tebakan awal untuk medan kecepatan dan tekanan. Dengan menyebut tebakan awal atau solusi pada awal iterasi apa pun dengan superskrip (n), maka medan kecepatan dan tekanan sementara diberikan oleh u(n) dan p (n). Pada setiap iterasi, dengan menyelesaikan persamaan momentum terlebih dahulu untuk medan kecepatan, solusi yang diperoleh ditandai dengan superskrip * karena bukan solusi akhir pada iterasi saat ini. Dengan demikian, persamaan momentum memenuhi

di mana medan tekanan masih didasarkan pada nilai-nilai dari iterasi sebelumnya. Medan kecepatan yang dihitung u* memenuhi persamaan momentum tetapi tidak selalu persamaan kontinuitas, karena medan tekanan tidak tepat. Oleh karena itu, koreksi dicari untuk memastikan bahwa medan kecepatan (atau laju aliran massa) dan medan tekanan memenuhi persamaan kontinuitas. Dengan menyebut medan koreksi dengan superskrip prime, yaitu (u’,p’), maka medan kecepatan dan tekanan yang dicari diberikan oleh
Perhatikan bahwa laju aliran massa di wajah sel juga akan dikoreksi sesuai dengan

sehingga laju aliran massa yang tepat memenuhi persamaan kontinuitas, yaitu

yang dapat ditulis ulang sebagai

Ini adalah bentuk yang menarik dari persamaan kontinuitas yang menunjukkan bahwa begitu laju aliran massa yang dihitung mencapai solusi yang tepat dan memenuhi persamaan kontinuitas, maka RHS menjadi nol menyebabkan medan koreksi menjadi nol. Oleh karena itu, kesalahan konservasi massa dari medan saat ini yang mendorong medan koreksi. Laju aliran massa dan koreksi laju aliran massa pada wajah elemen diberikan oleh

dan

di mana dalam Persamaan (15.32) dan (15.33) fakta bahwa 𝑆𝑒𝑥=∆𝑦𝑒 𝑑𝑎𝑛 𝑆𝑤𝑥=−∆𝑦𝑤telah digunakan. Medan tekanan tidak muncul dalam Persamaan (15.31) dan untuk memasukkannya ke dalam persamaan, bentuk diskret dari persamaan momentum digunakan. Proses ini dimulai dengan menuliskan kembali Persamaan (15.26) dalam bentuk yang lebih ringkas sebagai

Dimana

Untuk kasus medan kecepatan yang dihitung, persamaan di atas dituliskan sebagai

Dengan mengurangi persamaan momentum yang dihitung, Persamaan (15.36), dari persamaan yang tepat, Persamaan (15.34), diperoleh persamaan untuk medan koreksi sebagai

Pendekatan serupa digunakan untuk w face menghasilkan

Dengan mensubstitusikan Persamaan (15.33) ke dalam persamaan kontinuitas, Persamaan (15.31), bentuknya yang diperluas menjadi
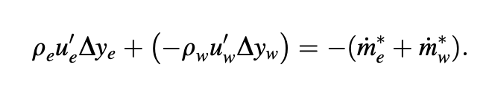
Kemudian mengganti bentuk diskret dari u'e dan u'w yang dihitung dari Persamaan (15.37) dan (15.38), masing-masing, dalam Persamaan (15.39), diperoleh persamaan yang melibatkan koreksi tekanan dan diberikan oleh

Dalam persamaan ini, medan tekanan muncul dalam bentuk yang mirip difusi, yang setelah diskritisasi menjadi

atau

Dengan mengatur ulang, persamaan koreksi tekanan diformulasikan sebagai

dimana

