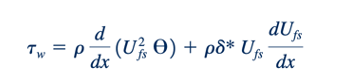Persamaan Lapisan Batas Integral Momentum dengan Gradien Tekanan Bukan Nol
Hasil lapisan batas yang dibahas dalam Bagian 9.2.2 dan 9.2.3 hanya berlaku untuk lapisan batas dengan gradien tekanan nol. Mereka sesuai dengan profil kecepatan yang ditandai sebagai C dalam Fig. 9.17b. Karakteristik lapisan batas untuk aliran dengan gradien tekanan non-nol dapat diperoleh dari persamaan lapisan batas parsial non-linear, serupa dengan Persamaan 9.8 dan 9.9, dengan memperhitungkan gradien tekanan yang sesuai. Pendekatan seperti itu berada di luar cakupan buku ini (Ref. 1, 2).
Salah satu pendekatan alternatif adalah memperluas teknik persamaan integral momentum lapisan batas (Bagian 9.2.3) agar berlaku untuk aliran dengan gradien tekanan non-nol. Persamaan integral momentum untuk aliran lapisan batas dengan gradien tekanan nol, Persamaan 9.26, adalah pernyataan tentang keseimbangan antara gaya gesek pada pelat (diwakili oleh 𝜏𝑤) dan laju perubahan momentum dari fluida dalam lapisan batas [diwakili oleh pU^2 (d𝜃/dx)]. Untuk aliran tersebut, kecepatan alir bebasnya konstan (Ufs = U). Jika kecepatan alir bebas tidak konstan [Ufs = Ufs(x), di mana x adalah jarak yang diukur sepanjang benda melengkung], tekanan tidak akan konstan. Hal ini mengikuti dari persamaan Bernoulli dengan efek gravitasi yang diabaikan, karena p+pU2fs/2 konstan sepanjang garis aliran di luar lapisan batas. Dengan demikian,
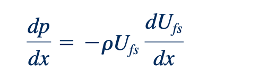
Untuk suatu benda tertentu, kecepatan alir bebas dan gradien tekanan yang sesuai pada permukaan dapat diperoleh dari teknik aliran tanpa viskos (aliran potensial) yang dibahas dalam Bagian 6.7. (Inilah cara hasil silinder lingkaran dari Gambar 9.16 diperoleh.)
Aliran dalam lapisan batas dengan gradien tekanan non-nol sangat mirip dengan yang ditunjukkan dalam Gambar 9.11, kecuali bahwa kecepatan alir hulu, U, digantikan oleh kecepatan alir bebas, Ufs(x), dan tekanan pada bagian (1) dan (2) tidak selalu sama. Dengan menggunakan komponen x dari persamaan momentum 1Persamaan 5.222 dengan gaya gesek dan gaya tekanan yang sesuai yang bertindak pada permukaan kontrol yang ditunjukkan dalam Gambar 9.11, persamaan momentum integral berikut untuk aliran lapisan batas diperoleh: