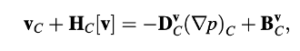Persamaan Momentum Terdiskritisasi
Persamaan momentum yang diberikan oleh Persamaan (15.2) dimodifikasi sedikit dan ditulis sebagai
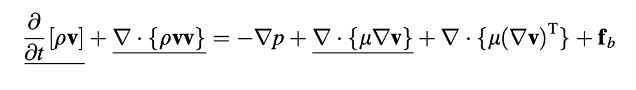
Forma terdiskrit Persamaan (15.64) dalam interval waktu [t - Δt/2, t + Δt/2] dicari di atas elemen C yang ditunjukkan dalam Gambar 15.15.
Dalam Persamaan (15.64), tiga ekspresi yang digarisbawahi mewakili, dari kiri ke kanan, adalah istilah tidak stabil, konveksi, dan difusi, secara berturut-turut. Diskritisasi dari istilah-istilah ini dilakukan seperti yang disajikan dalam bab-bab sebelumnya. Istilah-istilah yang tersisa dievaluasi secara eksplisit dan diperlakukan sebagai sumber. Integral volume dari bagian kedua istilah tegangan geser diubah menjadi integral permukaan menggunakan teorema divergensi dan kemudian menjadi jumlah fluks permukaan sebagai
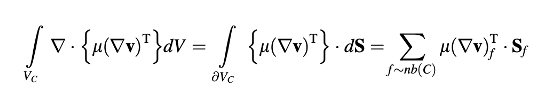
di mana bentuk yang diperluas dari (∇𝑣)𝑓𝑇 dalam sistem koordinat tiga dimensi diberikan oleh
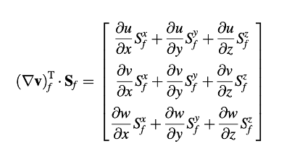
Integral volume dari gradien tekanan juga diperlakukan sebagai istilah sumber dan dievaluasi secara eksplisit sebagai
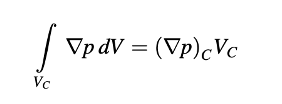
atau diubah menjadi integral permukaan sesuai dengan Persamaan (2.85) dan dihitung sebagai
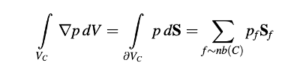
Istilah gaya tubuh diintegrasikan langsung di atas volume kontrol untuk menghasilkan

Menggunakan skema Euler orde pertama untuk diskritisasi istilah tidak stabil, skema HR untuk istilah konveksi yang diimplementasikan melalui pendekatan koreksi tertunda, dan mendekomposisi fluks difusi menjadi bagian implisit yang sejajar dengan grid dan bagian difusi lintang eksplisit, persamaan momentum terdiskritisasi ditulis dalam bentuk vektor sebagai
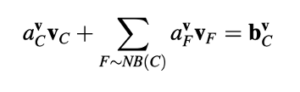
di mana koefisien diberikan oleh

dengan fluks permukaan dihitung menggunakan

dan fluks elemen dihitung dari
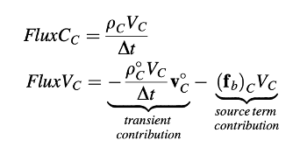
Meskipun bentuk aljabar dari persamaan momentum, Persamaan (15.70), linear, koefisien-koeifisiennya tergantung pada medan kecepatan dan tekanan. Nonlinearitas ini diatasi dengan proses iteratif di mana koefisien-koeffisien tersebut dihitung pada awal setiap iterasi berdasarkan nilai variabel-variabel tergantung yang diperoleh pada iterasi sebelumnya. Perubahan dalam nilai-nilai koefisien ini mengakibatkan perubahan besar dalam v dan mempengaruhi laju konvergensi hingga bahkan menyebabkan divergensi. Untuk memperlambat perubahan, relaksasi bawah dapat diterapkan ketika langkah-langkah waktu transien yang digunakan cukup besar. Menunjuk pada faktor relaksasi bawah dengan λv dan mengadopsi pendekatan relaksasi implisit Patankar, persamaan momentum yang direlaksasi bawah dapat ditulis sebagai:
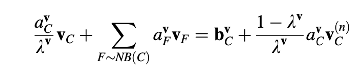
Dengan mendefinisikan kembali avC dan bvC sedemikian rupa sehingga
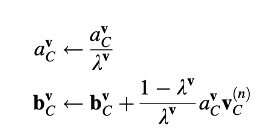
persamaan momentum yang direlaksasi bawah dapat ditulis ulang sebagai
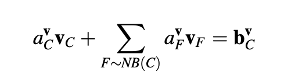
Untuk penurunan persamaan koreksi tekanan yang kolokasi, gradien tekanan diambil dari istilah sumber bvC dan ditampilkan secara eksplisit untuk menghasilkan
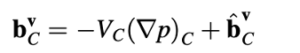
Mengganti kembali pada Persamaan (15.76), persamaan momentum menjadi
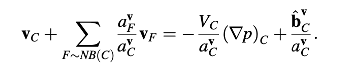
Defining the following vector operators:
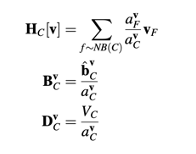
Persamaan (15.78) diformulasikan ulang sebagai