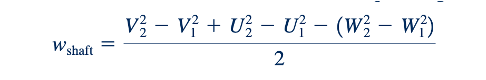Pertimbangan Dasar Momentum Sudut
Dalam bagian sebelumnya, kami mengindikasikan bagaimana transfer kerja ke atau dari fluida yang mengalir melalui sebuah pompa atau sebuah turbin terjadi melalui interaksi antara bilah rotor yang bergerak dan fluida. Karena semua turbomachine ini melibatkan rotasi impeller atau rotor sekitar sumbu sentral, adalah tepat untuk membahas kinerja mereka dalam hal torsi dan momentum sudut.
Ingat bahwa kerja dapat ditulis sebagai gaya kali jarak atau sebagai torsi kali perpindahan sudut. Oleh karena itu, jika torsi poros (torsi yang dihasilkan oleh poros pada rotor) dan rotasi rotor berada dalam arah yang sama, energi ditransfer dari poros ke rotor dan dari rotor ke fluida—mesin tersebut adalah pompa. Sebaliknya, jika torsi yang dihasilkan oleh poros pada rotor berlawanan dengan arah rotasi, transfer energi adalah dari fluida ke rotor—sebuah turbin. Jumlah torsi poros (dan, karenanya, kerja poros) dapat diperoleh dari persamaan momen-momentum yang diturunkan secara formal dalam Bagian 5.2.3 dan dibahas sebagai berikut.
Pertimbangkan sebuah partikel fluida yang bergerak keluar melalui rotor dalam mesin aliran radial yang ditunjukkan dalam Gambar E12.1a, b, dan c. Untuk saat ini, asumsikan bahwa partikel masuk ke rotor hanya dengan kecepatan radial saja (tanpa "swirl"). Setelah dipengaruhi oleh bilah rotor selama perjalanan dari inlet [bagian (1)] ke outlet [bagian (2)], partikel ini keluar dengan komponen kecepatan radial (r) dan komponen sirkumferensial (u). Dengan demikian, partikel masuk tanpa momentum sudut sekitar sumbu rotasi rotor tetapi keluar dengan momentum sudut yang tidak nol sekitar sumbu tersebut. (Ingat bahwa komponen aksial momentum sudut untuk sebuah partikel adalah massa partikel dikali jarak dari sumbu dikali komponen kecepatan absolut u.)
Pertimbangkan pengalaman serupa yang bisa terjadi di taman bermain di lingkungan sekitar. Bayangkan dirimu sebagai sebuah partikel dan perosotan berputar sebagai rotor. Berjalanlah dari tengah ke pinggir perosotan berputar dan perhatikan gaya yang terlibat. Perosotan berputar melakukan pekerjaan padamu — ada "gaya ke samping" pada dirimu. Orang lain harus menerapkan gaya torsi (dan daya) pada perosotan berputar untuk menjaga kecepatan sudut tetap konstan; jika tidak, momentum sudut sistem (dirimu dan perosotan berputar) akan terpelihara, dan kecepatan sudut akan menurun saat kamu meningkatkan jarakmu dari sumbu rotasi. (Demikian juga, jika motor yang menggerakkan pompa dimatikan, pompa tentu akan melambat dan berhenti. Temanmu adalah motor yang menyuplai energi ke rotor yang kemudian ditransfer kepadamu.) Apakah jumlah energi yang dikeluarkan oleh temanmu untuk menjaga kecepatan sudut tetap konstan tergantung pada jalur yang kamu tempuh di sepanjang perosotan berputar (misalnya, bentuk bilah), pada seberapa cepat dan ke arah mana kamu berjalan ke tepi (misalnya, kecepatan keluar), atau pada berat badanmu (misalnya, kerapatan fluida)? Apa yang terjadi jika kamu berjalan dari pinggir luar menuju ke pusat perosotan berputar yang berputar? Ingatlah bahwa kebalikan dari sebuah pompa adalah sebuah turbin.
Dalam sebuah turbomachine, serangkaian partikel (sebuah kontinum) melewati rotor. Oleh karena itu, persamaan momen-momentum yang diterapkan pada volume kontrol sebagaimana yang diturunkan di Bagian 5.2.3 berlaku. Untuk aliran steady (atau untuk rotor turbomachine dengan aliran siklik yang steady dalam rata-rata), Persamaan 5.42 memberikan:
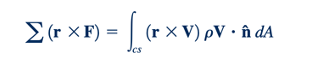
Ingatlah bahwa bagian kiri persamaan ini mewakili jumlah torsi (moments) eksternal yang bertindak pada isi volume kontrol, dan bagian kanan adalah laju bersih aliran momen-momentum (momentum sudut) melalui permukaan kontrol.
Komponen aksial dari persamaan ini yang diterapkan pada penyederhanaan satu dimensi aliran melalui rotor turbomachine dengan bagian (1) sebagai masukan dan bagian (2) sebagai keluaran menghasilkan
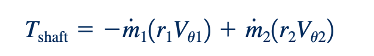
di mana Tshaft adalah torsi poros yang diterapkan pada isi volume kontrol. “-” terkait dengan laju aliran massa ke dalam volume kontrol, dan “ + ” digunakan dengan aliran keluar. Tanda dari komponen Vu bergantung pada arah V𝜃 dan gerakan bilah, U. Jika V𝜃 dan U searah, maka V𝜃 positif. Tanda torsi yang diberikan oleh poros pada rotor, Tshaft, positif jika Tshaft searah dengan putaran, dan negatif jika sebaliknya.
Seperti yang terlihat dari Persamaan 12.2, torsi poros berbanding lurus dengan laju aliran massa, m = pQ. Torsi juga bergantung pada komponen tangensial dari kecepatan absolut, V𝜃. Persamaan 12.2 sering disebut sebagai persamaan turbomachine Euler.
Juga diingat bahwa daya poros, Wshaft, berkaitan dengan torsi poros dan kecepatan sudut oleh
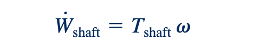
Dengan menggabungkan Persamaan 12.2 dan 12.3 serta menggunakan fakta bahwa U = wr, kita dapatkan
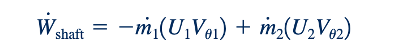
Kembali, nilai V𝜃 positif ketika V𝜃 dan U bergerak ke arah yang sama dan negatif sebaliknya. Begitu pula, W positif ketika torsi poros dan v bergerak ke arah yang sama dan negatif sebaliknya. Oleh karena itu, W poros positif ketika daya disalurkan ke isi volume kontrol (pompa) dan negatif sebaliknya (turbina). Hasil ini konsisten dengan konvensi tanda yang melibatkan istilah kerja dalam persamaan energi yang dipertimbangkan dalam Bab 5 (lihat Persamaan 5.67).
Akhirnya, dalam hal kerja per satuan massa, Wporos = Wporos /m, yang memberikan:
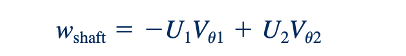
Di mana kita telah menggunakan fakta bahwa berdasarkan hukum kekekalan massa, m1 sama dengan m2. Persamaan 12.3, 12.4, dan 12.5 adalah persamaan dasar yang mengatur untuk pompa atau turbin, baik mesin tersebut adalah perangkat aliran radial, campuran, atau aksial, dan untuk aliran yang dapat dipadatkan maupun tidak dapat dipadatkan. Perhatikan bahwa baik komponen aksial maupun radial dari kecepatan masuk ke dalam persamaan kerja spesifik. [Dalam contoh merry-go-round di atas, jumlah pekerjaan yang dilakukan oleh teman Anda tidak bergantung pada seberapa cepat Anda melompat "ke atas" (aksial) atau "keluar" (radial) saat Anda keluar. Satu-satunya hal yang penting adalah komponen kecepatan u Anda.]
Bentuk lain dari Persamaan 12.5 yang lebih berguna tetapi lebih rumit dapat diperoleh dengan menuliskan bagian kanan dalam bentuk yang sedikit berbeda berdasarkan segitiga kecepatan di pintu masuk atau keluar seperti yang ditunjukkan secara umum dalam Gambar 12.5. Komponen kecepatan Vx adalah komponen kecepatan aliran melalui secara umum, dan itu bisa aksial, radial, atau di antaranya tergantung pada konfigurasi rotor. Dari segitiga besar di sisi kanan, kita dapat melihat bahwa:
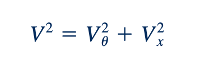
Atau
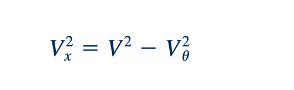

Dari segitiga kecil di sisi kanan, kita dapat melihat bahwa:

Dengan menggabungkan Persamaan 12.6 dan 12.7, kita mendapatkan:
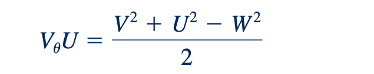
yang jika dituliskan untuk masukan dan keluaran dan digabungkan dengan Persamaan 12.5 memberikan: