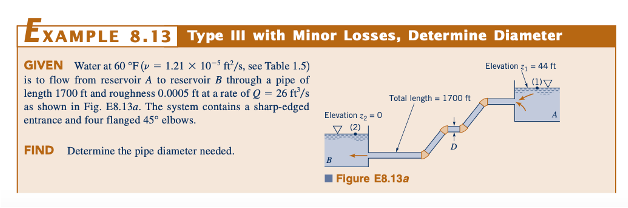
Pipa Tunggal
Proses penyelesaian masalah aliran pipa dapat sangat dipengaruhi oleh parameter mana yang dianggap independen (yang "diberikan") dan mana yang bergantung (yang "ditentukan"). Tiga jenis masalah paling umum diuraikan dalam Tabel 8.4 dalam hal parameter yang terlibat. Kami biasanya menentukan sistem pipa dalam hal panjang bagian pipa yang digunakan dan jumlah siku, tikungan, dan katup yang diperlukan untuk membawa fluida antara lokasi yang diinginkan. Dalam semua kasus, kami mengasumsikan bahwa properti fluida telah diberikan.
Dalam masalah Tipe I, kami menentukan laju aliran atau kecepatan rata-rata yang diinginkan dan menentukan perbedaan tekanan atau kerugian kepala yang diperlukan. Sebagai contoh, jika laju aliran sebesar 2.0 galon per menit diperlukan untuk mesin pencuci piring yang terhubung ke pemanas air melalui sistem pipa yang diberikan seperti yang ditunjukkan oleh gambar di sisi, berapa tekanan yang diperlukan di pemanas air?
Dalam masalah Tipe II, kami menentukan tekanan penggerak yang diberikan (atau, sebagai alternatif, kerugian kepala) dan menentukan laju aliran. Sebagai contoh, berapa banyak galon per menit air panas yang disuplai ke mesin pencuci piring jika tekanan dalam pemanas air adalah 60 psi dan detail sistem pipa (panjang, diameter, kasar pipa; jumlah siku; dll.) ditentukan?
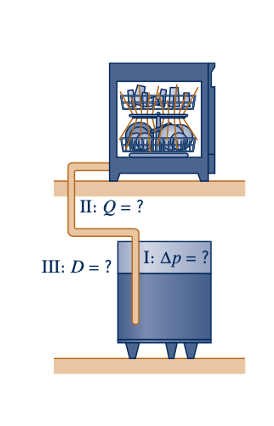

Dalam masalah Tipe III, kami menentukan penurunan tekanan dan laju aliran, lalu menentukan diameter pipa yang diperlukan. Sebagai contoh, berapa diameter pipa yang diperlukan antara pemanas air dan mesin pencuci piring jika tekanan di pemanas air adalah 60 psi (ditentukan oleh sistem air kota) dan laju alirannya tidak boleh kurang dari 2,0 galon per menit (ditentukan oleh produsen)?
Beberapa contoh masalah seperti ini akan diuraikan selanjutnya.



Meskipun persamaan aliran pipa yang mengaturnya cukup sederhana, mereka dapat memberikan hasil yang sangat masuk akal untuk berbagai aplikasi, seperti yang ditunjukkan dalam contoh berikut.


Masalah aliran pipa di mana ingin ditentukan laju aliran untuk serangkaian kondisi yang diberikan (Masalah Tipe II) seringkali memerlukan teknik trial-and-error atau pencarian akar numerik. Hal ini karena perlu untuk mengetahui nilai faktor gesekan untuk melakukan perhitungan, tetapi faktor gesekan adalah fungsi dari kecepatan yang tidak diketahui (laju aliran) dalam hal bilangan Reynolds. Prosedur penyelesaiannya dijelaskan dalam Contoh 8.10.




Dalam masalah aliran pipa di mana diameter adalah yang tidak diketahui (Tipe III), diperlukan teknik pencarian akar iteratif atau numerik. Ini, sekali lagi, karena faktor gesekan adalah fungsi dari diameter—melalui baik jumlah Reynolds maupun ketebalan relatif. Oleh karena itu, baik Re = 𝜌𝑉𝐷/𝜇 =4pQ/𝜋𝜇𝐷 juga tbukan 𝜀/𝐷 tidak diketahui kecuali D diketahui. Contoh 8.12 dan 8.13 mengilustrasikannya.

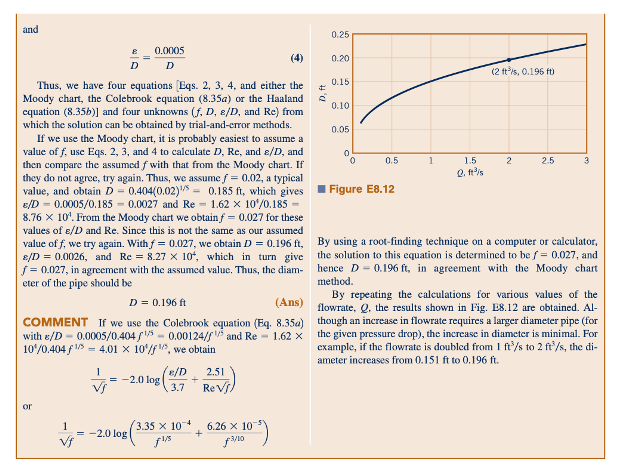
Pada contoh sebelumnya, kita hanya perlu mempertimbangkan kerugian utama. Dalam beberapa kasus, penambahan kerugian utama dan minor dapat menyebabkan prosedur solusi yang sedikit lebih panjang, meskipun persamaan yang mengatur pada dasarnya sama. Ini diilustrasikan dalam Contoh 8.13.