Profil Kecepatan Turbulen
Banyak informasi tentang profil kecepatan turbulen telah diperoleh melalui analisis dimensional, eksperimen, simulasi numerik, dan upaya teoretis semi-empiris. Seperti yang ditunjukkan dalam Fig. 8.15, aliran turbulen yang sepenuhnya berkembang dalam pipa dapat dibagi menjadi tiga wilayah yang ditandai oleh jarak mereka dari dinding: lapisan subviskus yang sangat dekat dengan dinding pipa, wilayah tumpang tindih, dan lapisan turbulen luar di seluruh bagian tengah aliran. Dalam lapisan subviskus, tegangan geser viskus mendominasi dibandingkan dengan tegangan turbulen (atau Reynolds), dan sifat aliran yang berputar acak secara praktis tidak ada. Di lapisan turbulen luar, tegangan Reynolds mendominasi, dan ada pencampuran dan keacakan yang cukup dalam aliran.
Karakter aliran dalam dua wilayah ini benar-benar berbeda. Misalnya, dalam lapisan subviskus, viskositas fluida adalah parameter penting; kepadatan tidak penting. Di lapisan luar, kebalikannya terjadi. Dengan menggunakan argumen analisis dimensional yang hati-hati untuk aliran di setiap lapisan dan dengan mencocokkan hasil di lapisan tumpang tindih yang umum, telah memungkinkan untuk mendapatkan kesimpulan berikut tentang profil kecepatan turbulen dalam pipa halus.
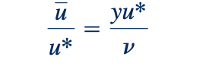

di mana y=R−r adalah jarak yang diukur dari dinding, u adalah komponen kecepatan x yang diaverasi dalam waktu, dan u∗ = τ w/ρ disebut kecepatan gesekan. Perhatikan bahwa u∗ bukanlah kecepatan aktual dari fluida - itu hanyalah kuantitas yang memiliki dimensi kecepatan. Seperti yang ditunjukkan dalam Fig. 8.16, Persamaan 8.29 (biasanya disebut sebagai hukum dinding) berlaku sangat dekat dengan dinding halus, untuk 0<y<u ∗/ν=y + <5. Argumen analisis dimensional menunjukkan bahwa dalam wilayah tumpang tindih, kecepatan seharusnya bervariasi sebagai logaritma dari y. Oleh karena itu, ungkapan berikut telah diusulkan:
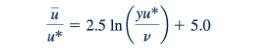
di mana konstan 2.5 dan 5.0 telah ditentukan secara eksperimental. Seperti yang ditunjukkan dalam Fig. 8.16, untuk daerah yang tidak terlalu dekat dengan dinding halus, namun tidak sampai ke pusat pipa, Persamaan 8.30 memberikan korelasi yang masuk akal dengan data eksperimental. Perhatikan bahwa skala horizontal adalah skala logaritmik. Ini cenderung memperbesar ukuran lapisan subviskous relatif terhadap sisa aliran. Seperti yang ditunjukkan dalam Contoh 8.4, lapisan subviskous biasanya cukup tipis. Hasil serupa dapat diperoleh untuk aliran turbulen melewati dinding kasar.
Ada sejumlah korelasi lain untuk profil kecepatan dalam aliran pipa turbulen. Di wilayah pusat (lapisan turbulen luar), ungkapan Vc −u=2.5ln(yR), di mana Vc adalah kecepatan garis tengah, sering disarankan sebagai korelasi yang baik dengan data eksperimental. Korelasi lain yang sering digunakan (dan relatif mudah digunakan) adalah profil kecepatan hukum daya empiris
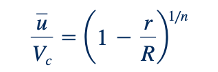
Dalam representasi ini, nilai n adalah fungsi dari nomor Reynolds, seperti yang ditunjukkan dalam Fig. 8.17. Profil kecepatan berdasarkan hukum daya satu-per-tujuh (n=71 ) sering digunakan sebagai perkiraan yang masuk akal untuk banyak aliran praktis. Profil kecepatan turbulen tipikal berdasarkan representasi hukum daya ini ditunjukkan dalam Fig. 8.18.
Pemeriksaan lebih lanjut terhadap Persamaan 8.31 menunjukkan bahwa profil hukum daya tidak dapat valid di dekat dinding, karena menurut persamaan ini gradien kecepatannya adalah tak terbatas di sana. Selain itu, Persamaan 8.31 tidak dapat persis valid di dekat garis tengah karena tidak memberikan dr/du =0 saat r=0. Namun, ini memberikan perkiraan yang masuk akal untuk profil kecepatan yang diukur di sebagian besar pipa.
Perhatikan dari Fig. 8.18 bahwa profil turbulen jauh lebih "datar" daripada profil laminar dan bahwa kelurusan ini meningkat dengan nomor Reynolds (yaitu, dengan n2). Ingat dari Bab 3 bahwa

Hasil perkiraan yang masuk akal sering kali diperoleh dengan menggunakan persamaan Bernoulli tak kental dan dengan mengasumsikan profil kecepatan seragam fiktif. Karena sebagian besar aliran bersifat turbulen dan aliran turbulen cenderung memiliki profil kecepatan yang hampir seragam, maka kegunaan persamaan Bernoulli dan asumsi profil seragam tidak mengherankan. Tentu saja, banyak sifat aliran yang tidak dapat dijelaskan tanpa memperhitungkan efek kental.


