Pusaran
Selanjutnya, kita pertimbangkan medan aliran di mana garis-garis aliran adalah lingkaran-linakran konsentris - dengan kata lain, kita tukar antara potensial kecepatan dan fungsi arus untuk sumber. Oleh karena itu, kita misalkan

Dan
dimana K adalah sebuah konstanta. Dalam hal ini, garis-garis aliran adalah lingkaran-linakran konsentris, seperti yang diilustrasikan dalam Figur 6.18, dengan vr = 0 dan


Hasil ini menunjukkan bahwa kecepatan tangensial bervariasi secara terbalik dengan jarak dari asal, seperti yang ditunjukkan oleh gambar di samping, dengan sebuah singularitas terjadi pada r=0 (di mana kecepatan menjadi tak terhingga).
Mungkin terdengar aneh bahwa gerakan pusaran ini irrotasional (dan itu memang demikian karena medan aliran dijelaskan oleh potensial kecepatan). Namun, perlu diingat bahwa rotasi merujuk pada orientasi sebuah elemen fluida dan bukan pada jalur yang diikuti oleh elemen tersebut. Dengan demikian, untuk pusaran irrotasional, jika sepasang stik kecil ditempatkan dalam medan aliran di lokasi A, seperti yang ditunjukkan dalam Figur 6.19a, stik-stik tersebut akan berputar saat mereka bergerak ke lokasi B. Salah satu stik, yang sejajar dengan garis aliran, akan mengikuti lintasan melingkar dan berputar searah jarum jam.


Stik yang lain akan berputar dalam arah searah jarum jam karena sifat medan aliran — bagian stik yang terdekat dengan asal bergerak lebih cepat daripada ujung yang berlawanan. Meskipun kedua stik berputar, rata-rata kecepatan sudut kedua stik adalah nol karena aliran bersifat irrotasional.
Jika fluida berputar sebagai badan yang kaku, sehingga v𝜃= K1r dimana K1 adalah sebuah konstanta, maka stik-stik yang ditempatkan pada medan aliran akan berputar seperti yang diilustrasikan dalam Gambar 6.19b. Jenis gerakan pusaran ini bersifat rotasional dan tidak dapat dijelaskan dengan potensial kecepatan. Pusaran rotasional ini umumnya disebut sebagai pusaran paksa, sedangkan pusaran irrotasional biasanya disebut sebagai pusaran bebas. Gerakan berputar air saat mengalir keluar dari bak mandi mirip dengan pusaran bebas, sedangkan gerakan cairan yang terkandung dalam tangki yang diputar sepanjang sumbunya dengan kecepatan sudut v sesuai dengan pusaran paksa.
Sebuah pusaran gabungan adalah pusaran yang memiliki pusaran paksa sebagai inti pusat dan distribusi kecepatan yang sesuai dengan pusaran bebas di luar inti tersebut. Dengan demikian, untuk sebuah pusaran gabungan

Dan

di mana K dan v adalah konstanta, dan r0 merupakan radius inti pusat. Distribusi tekanan baik pada pusaran bebas maupun pusaran paksa sebelumnya telah dipertimbangkan dalam Contoh 3.3. (Lihat Gambar E6.6a untuk perkiraan jenis aliran ini.)

Konsep matematika yang umumnya terkait dengan gerakan pusaran adalah sirkulasi. Sirkulasi, Γ, didefinisikan sebagai integral garis dari komponen tangensial dari kecepatan yang diambil sepanjang kurva tertutup dalam medan aliran. Dalam bentuk persamaan, sirkulasi dapat diekspresikan sebagai:

di mana tanda integral berarti bahwa integrasi diambil sepanjang kurva tertutup, C, dalam arah berlawanan arah jarum jam, dan ds adalah panjang diferensial sepanjang kurva seperti yang diilustrasikan dalam Gambar 6.20. Untuk aliran irrotasional, V=∇ϕ sehingga V⋅ds=∇ϕ⋅ds=dϕ dan, oleh karena itu,

Hasil ini menunjukkan bahwa untuk aliran irrotasional, sirkulasi umumnya akan nol. (Bab 9 memiliki diskusi lebih lanjut tentang sirkulasi dalam aliran nyata.) Namun, jika terdapat singularitas yang terkandung dalam kurva, sirkulasi mungkin tidak nol. Sebagai contoh, untuk pusaran bebas dengan v∝r, sirkulasi sepanjang jalur lingkaran dengan radius r seperti yang ditunjukkan dalam Gambar 6.21 adalah:
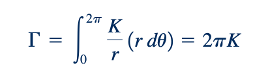
Ini menunjukkan bahwa sirkulasi tidak nol dan konstanta K=2π. Namun, untuk aliran irrotasional, sirkulasi sepanjang jalur apapun yang tidak termasuk titik singular akan nol. Ini dapat dengan mudah dikonfirmasi untuk jalur tertutup ABCD pada Gambar 6.21 dengan mengevaluasi sirkulasi sepanjang jalur tersebut.
Potensial kecepatan dan fungsi aliran untuk pusaran bebas umumnya dinyatakan dalam bentuk sirkulasi sebagai berikut:

Dan

Konsep sirkulasi seringkali berguna saat mengevaluasi gaya yang berkembang pada benda yang terendam dalam fluida bergerak. Aplikasi ini akan dipertimbangkan dalam Bagian 6.6.3.


