Rankine Oval - infistream

Rankine Oval

Setengah tubuh yang dijelaskan dalam bagian sebelumnya adalah sebuah tubuh yang "terbuka" di satu ujung. Untuk mempelajari aliran di sekitar tubuh tertutup, sebuah sumber dan sebuah sumur dengan kekuatan yang sama dapat digabungkan dengan aliran seragam seperti yang ditunjukkan dalam Gambar 6.25a. Fungsi arus untuk kombinasi ini adalah:

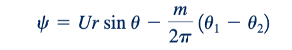
dan potensial kecepatannya adalah:

Seperti yang dibahas dalam Bagian 6.5.4, fungsi arus untuk pasangan sumber-sumur dapat dinyatakan seperti dalam Persamaan 6.93, dan, oleh karena itu, Persamaan 6.103 juga dapat ditulis sebagai

Atau

Garis aliran yang sesuai untuk medan aliran ini diperoleh dengan menetapkan 𝜓=konstan. Jika beberapa garis aliran ini diplot, akan terlihat bahwa garis aliran 𝜓 = 0 membentuk sebuah tubuh tertutup seperti yang diilustrasikan dalam Gambar 6.25b. Kita dapat menganggap garis aliran ini sebagai permukaan dari sebuah tubuh dengan panjang 2ℓ dan lebar 2h yang ditempatkan dalam aliran seragam. Garis-garis aliran di dalam tubuh tidak menarik secara praktis dan tidak ditunjukkan. Perlu diperhatikan bahwa karena tubuh tertutup, semua aliran yang berasal dari sumber mengalir ke dalam sumur. Tubuh-tubuh ini memiliki bentuk oval dan disebut sebagai oval Rankine.

Titik stagnasi terjadi di ujung hulu dan ujung hilir dari tubuh, seperti yang ditunjukkan dalam Gambar 6.25b. Titik-titik ini dapat ditemukan dengan menentukan di mana kecepatan nol sepanjang sumbu x. Titik-titik stagnasi sesuai dengan titik-titik di mana kecepatan seragam, kecepatan sumber, dan kecepatan sumur semua digabungkan untuk memberikan kecepatan nol. Lokasi titik-titik stagnasi tergantung pada nilai a, m, dan U. Separuh panjang tubuh, ℓ (nilai |𝑥| yang memberikan V=0 ketika y=0), dapat dinyatakan sebagai:

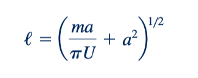
Atau

Separuh lebar tubuh, ℎ, dapat diperoleh dengan menentukan nilai y di mana sumbu y berpotongan dengan garis aliran 𝜓=0. Dengan demikian, dari Persamaan 6.105 dengan 𝜓=0, x=0, dan y=h, maka diperoleh bahwa:

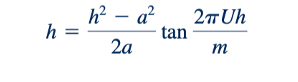
Atau

Persamaan 6.107 dan 6.109 menunjukkan bahwa baik l/a maupun ℎ/a adalah fungsi dari parameter tak berdimensi, 𝜋Ua/m . Meskipun untuk nilai tertentu dari Ua/m nilai yang sesuai dari l/a dapat ditentukan secara langsung dari Persamaan 6.107, h/a harus ditentukan melalui solusi uji-coba dari Persamaan 6.109.

Berbagai bentuk tubuh dengan rasio panjang terhadap lebar yang berbeda dapat diperoleh dengan menggunakan nilai Ua/m yang berbeda, seperti yang ditunjukkan oleh gambar di pinggiran. Saat parameter ini menjadi besar, aliran di sekitar tubuh yang panjang dan ramping dijelaskan, sedangkan untuk nilai kecil dari parameter tersebut, aliran di sekitar lebih tumpul diperoleh. Di sebelah hilir dari titik lebar tubuh maksimum, tekanan permukaan meningkat seiring jarak di sepanjang permukaan. Kondisi ini (disebut gradien tekanan yang tidak menguntungkan) biasanya menyebabkan terpisahnya aliran dari permukaan, yang menghasilkan pusaran tekanan rendah besar di sisi hilir tubuh. Pemisahan ini tidak diprediksi oleh teori potensial (yang hanya menunjukkan aliran simetris). Hal ini diilustrasikan oleh gambar di pinggir untuk bentuk yang sangat tumpul, yang menunjukkan perbedaan antara aliran potensial dan aliran viskos. Oleh karena itu, solusi potensial untuk oval Rankine akan memberikan perkiraan yang masuk akal dari kecepatan di luar lapisan batas viskos tipis dan distribusi tekanan hanya pada bagian depan tubuh.