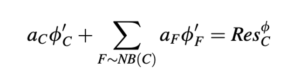Residual Form of the Equation - infistream

Residual Form of the Equation

Sejauh ini, persamaan aljabar yang terdiskritisasi telah ditulis dalam bentuk "langsung" atau "standar" sebagai

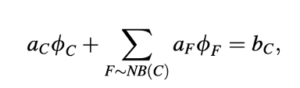
Persamaan (14.19) juga dapat ditulis dalam bentuk "koreksi" atau "residu" dengan mengatur ulang term-term sehingga memungkinkan untuk menyelesaikan koreksi yang diperlukan untuk memenuhi persamaan tersebut. Jika ∅𝐶* dan ∅'𝑐 adalah nilai iterasi sebelumnya dari ∅𝑐 dan koreksi yang diperlukan untuk memenuhi Persamaan (14.19), maka solusinya diberikan oleh

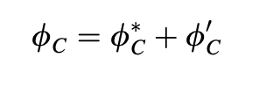
dan Persamaan (14.19) dapat ditulis ulang sebagai

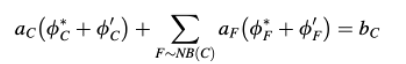
Atau

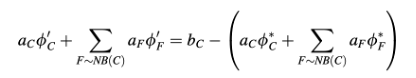
Perhatikan bahwa sisi kanan Persamaan (14.22) mewakili kesalahan residu dari persamaan untuk medan ∅𝑐*. Dengan menunjukkan residu ini di atas elemen C dengan Re𝑠𝑐∅, Persamaan (14.22) menjadi

Harus dicatat bahwa untuk medan yang tepat, Re𝑠𝐶∅ akan nol.

Meskipun secara matematis setara dengan Persamaan (14.19), Persamaan (14.23) memiliki satu keuntungan numerik. Dalam bentuk ini, kesalahan numerik selama penyelesaian persamaan sedikit lebih kecil daripada yang terkait dengan bentuk standar untuk kasus ketika variasi kecil diharapkan untuk nilai besar dari ∅.

14.3.1 Residual Form of Patankar’s Under-Relaxation

Open chat

Hello 👋
Thank you for text me
Can we help you?