REYNOLDS TRANSPORT THEOREM
Hukum-hukum konservasi yang disebutkan di atas berlaku untuk volume material yang bergerak dari fluida (Gambar 3.1), dan bukan untuk titik tetap atau volume kontrol. Untuk mengekspresikan hukum-hukum ini mengikuti pendekatan Eulerian, diperlukan untuk mengetahui ekuivalen Eulerian dari integral yang diambil atas volume material yang bergerak dari fluida. Ini diberikan melalui teorema transportasi Reynolds.
Rumus konversi sedikit berbeda tergantung pada apakah volume kontrol tersebut tetap, bergerak, atau deformabel. Untuk mendapatkan rumus ini, biarkan B menjadi properti apa pun dari fluida (massa, momentum, energi, dll.) dan biarkan b = dB/dm menjadi nilai intensif dari B (jumlah B per satuan massa) dalam elemen kecil apa pun dari fluida. Untuk volume kontrol yang bergerak dan deformabel yang ditunjukkan dalam Gambar 3.1, perubahan total seketika dari B dalam volume material (MV) sama dengan perubahan total seketika dari B dalam volume kontrol (V) ditambah dengan aliran bersih dari B masuk dan keluar dari volume kontrol melalui permukaan kontrolnya (S). Biarkan ρ menyatakan kerapatan fluida, n adalah normal keluar ke permukaan volume kontrol, v(t, x) adalah kecepatan fluida, vs(t, x) adalah kecepatan permukaan volume kontrol yang berdeformasi, dan vr(t, x) adalah kecepatan relatif di mana fluida memasuki/meninggalkan volume kontrol [yaitu, vr = v(t, x) – vs(t, x)], maka teorema transportasi Reynolds memberikan:
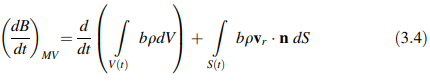
Untuk volume kontrol tetap, vs = 0 dan geometrinya independen terhadap waktu yang mengimplikasikan bahwa turunan waktu pada sisi kanan Persamaan (3.4) dapat ditulis menggunakan aturan Leibniz sebagai

Oleh karena itu, Persamaan (3.4) disederhanakan menjadi

Menerapkan teorema divergensi untuk mengubah integral permukaan menjadi integral volume, Persamaan (3.6) menjadi
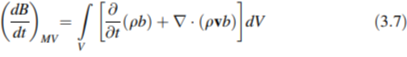
Suatu bentuk alternatif dari Persamaan (3.7) dapat diperoleh dengan mengembangkan suku kedua dalam tanda kurung siku dan menggunakan turunan substansial untuk mendapatkan

Persamaan (3.7) atau (3.8) dapat digunakan untuk mendapatkan bentuk Eulerian dari hukum konservasi dalam wilayah tetap.
