Sistem Beberapa Pipa
Pada banyak sistem pipa, terdapat lebih dari satu pipa yang terlibat. Sistem tabung yang kompleks dalam paru-paru kita (dimulai seperti yang ditunjukkan oleh gambar di pinggir halaman, dengan trakea berdiameter relatif besar dan berakhir di puluhan ribu bronkiolus kecil setelah banyak percabangan) dan labirin pipa dalam sistem distribusi air kota adalah contoh dari sistem-sistem semacam itu. Mekanisme pengaturan aliran dalam sistem pipa multipel sama dengan sistem pipa tunggal yang dibahas dalam bab ini. Namun, karena banyaknya variabel yang terlibat, kompleksitas tambahan mungkin muncul dalam memecahkan aliran dalam sistem pipa multipel. Beberapa kompleksitas ini dibahas dalam bagian ini.
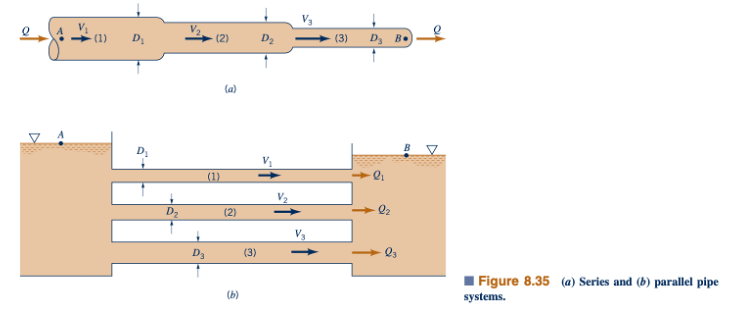
Sistem pipa multipel yang paling sederhana dapat diklasifikasikan menjadi aliran seri atau paralel, seperti yang ditunjukkan dalam Gambar 8.35. Nomenklatur ini mirip dengan yang digunakan dalam rangkaian listrik. Bahkan, sering kali dibuat analogi antara sirkuit fluida dan sirkuit listrik sebagai berikut. Dalam sirkuit listrik sederhana, terdapat keseimbangan antara tegangan (e), arus (i), dan hambatan (R) seperti yang diberikan oleh hukum Ohm: e = iR. Dalam sirkuit fluida, terdapat keseimbangan antara penurunan tekanan (∆p), laju aliran atau kecepatan (Q atau V), dan hambatan aliran yang dinyatakan dalam bentuk faktor gesekan dan koefisien kehilangan minor (f dan K). Untuk aliran sederhana, ∆p = f(1/4D^2)(ρV^2)/2, maka berlaku ∆p = QR, di mana R, suatu ukuran hambatan terhadap aliran, berbanding lurus dengan f.
Perbedaan utama antara metode penyelesaian yang digunakan untuk menyelesaikan masalah sirkuit listrik dan masalah sirkuit fluida terletak pada kenyataan bahwa hukum Ohm adalah persamaan linear (menggandakan tegangan menggandakan arus), sedangkan persamaan fluida umumnya bersifat nonlinear (menggandakan penurunan tekanan tidak menggandakan laju aliran kecuali alirannya laminar). Oleh karena itu, meskipun beberapa konsep dasar dan analogi dapat diterapkan antara keduanya, perbedaan dalam sifat matematis persamaan memerlukan pendekatan yang berbeda dalam penyelesaiannya.
Metode standar dalam rekayasa listrik dapat diterapkan untuk membantu menyelesaikan masalah mekanika fluida, sementara beberapa tidak dapat.
Salah satu sistem pipa ganda yang paling sederhana adalah yang berisi pipa-pipa secara berurutan, seperti yang ditunjukkan dalam Gambar 8.35a. Setiap partikel fluida yang melewati sistem melewati setiap pipa. Oleh karena itu, laju aliran (tetapi bukan kecepatan) sama di setiap pipa, dan kerugian kepala dari titik A ke titik B adalah jumlah dari kerugian kepala di setiap pipa. Persamaan yang mengatur dapat ditulis sebagai berikut:
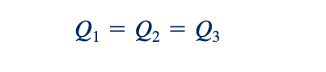
Dan
di mana subskrip merujuk pada masing-masing pipa. Secara umum, faktor friksi akan berbeda untuk setiap pipa karena jumlah Reynolds (Rei =pViDi/𝜇) dan kekasaran relatif (𝜀i/Di) akan berbeda. Jika laju aliran diberikan, maka perhitungan untuk menentukan kerugian kepala atau penurunan tekanan (masalah Tipe I) adalah langkah yang mudah dilakukan. Jika penurunan tekanan diberikan dan laju aliran harus dihitung (masalah Tipe II), maka diperlukan skema iterasi. Dalam situasi ini, tidak ada faktor gesekan yang diketahui, sehingga perhitungan mungkin melibatkan lebih banyak percobaan daripada sistem pipa tunggal yang sesuai. Hal yang sama berlaku untuk masalah di mana diameter pipa (atau diameter) harus ditentukan (masalah Tipe III).
Sistem pipa ganda lain yang umum berisi pipa-pipa sejajar, seperti yang ditunjukkan dalam Gambar 8.35b. Dalam sistem ini, partikel fluida yang bergerak dari A ke B dapat mengambil salah satu jalur yang tersedia, dengan total laju aliran sama dengan jumlah laju aliran di setiap pipa. Namun, dengan menulis persamaan energi antara titik A dan B, ditemukan bahwa kerugian kepala yang dialami oleh setiap partikel fluida yang bergerak antara lokasi ini adalah sama, independen dari jalur yang diambil. Dengan demikian, persamaan yang mengatur untuk pipa-pipa sejajar adalah:

Dan
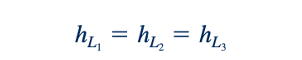
Kembali, metode penyelesaian persamaan ini tergantung pada informasi yang diberikan dan apa yang akan dihitung.
Jenis sistem pipa ganda lainnya disebut lingkaran dan ditunjukkan dalam Gambar 8.36. Dalam kasus ini, laju alir melalui pipa (1) sama dengan jumlah laju alir melalui pipa (2) dan (3), atau Q1 = Q2 + Q3. Seperti yang dapat dilihat dengan menuliskan persamaan energi antara permukaan masing-masing reservoir, kerugian kepala untuk pipa (2) harus sama dengan yang untuk pipa (3), meskipun ukuran pipa dan laju alir mungkin berbeda untuk masing-masing. Itulah,
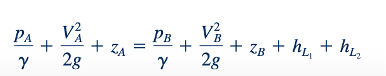
bagi partikel fluida yang melewati pipa (1) dan (2), sementara
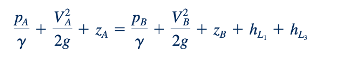
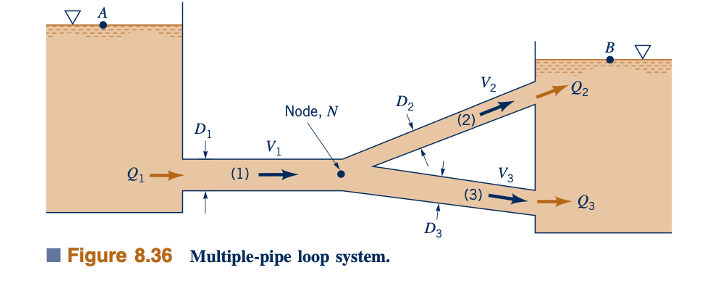

bagi fluida yang melewati pipa (1) dan (3). Ini dapat digabungkan untuk memberikan ℎ=ℎ L2 =hL3 . Ini merupakan pernyataan tentang kenyataan bahwa partikel-partikel fluida yang melewati pipa (2) dan partikel yang melewati pipa (3) semuanya berasal dari kondisi awal yang sama di persimpangan (atau simpul, N) pipa dan semuanya berakhir pada kondisi akhir yang sama.
Aliran dalam sistem pipa berganda yang terlihat relatif sederhana mungkin lebih kompleks daripada yang terlihat pada awalnya. Sistem percabangan yang disebut masalah tiga reservoir yang ditunjukkan dalam Gambar 8.37 adalah salah satu sistem tersebut. Tiga reservoir pada ketinggian yang diketahui dihubungkan bersama dengan tiga pipa yang memiliki properti yang diketahui (panjang, diameter, dan kasar permukaan). Masalahnya adalah untuk menentukan laju aliran masuk atau keluar dari reservoir. Jika katup (1) tertutup, fluida akan mengalir dari reservoir B ke C, dan laju alirnya dapat dengan mudah dihitung. Perhitungan serupa dapat dilakukan jika katup (2) atau (3) ditutup dengan yang lain terbuka.
Namun, dengan semua katup terbuka, tidak selalu jelas arah aliran fluida. Untuk kondisi yang ditunjukkan dalam Gambar 8.37, jelas bahwa fluida mengalir dari reservoir A karena kedua level reservoir lainnya lebih rendah. Baik fluida mengalir masuk atau keluar dari reservoir B tergantung pada elevasi reservoir B dan C serta properti (panjang, diameter, kasar permukaan) dari ketiga pipa. Secara umum, arah aliran tidak jelas, dan proses penyelesaiannya harus mencakup penentuan arah ini. Ini diilustrasikan dalam Contoh 8.14.


Sistem pipa yang paling kompleks adalah jaringan pipa seperti yang ditunjukkan dalam Gambar 8.38. Jaringan seperti ini sering terjadi dalam sistem distribusi air kota dan sistem lain yang mungkin memiliki banyak "inlet" dan "outlet". Arah aliran dalam berbagai pipa tidaklah jelas - sebenarnya, bisa berbeda dari waktu ke waktu, tergantung pada bagaimana sistem tersebut digunakan dari waktu ke waktu.
Penyelesaian untuk masalah jaringan pipa sering dilakukan dengan menggunakan persamaan node dan loop yang mirip dalam banyak hal dengan yang dilakukan dalam rangkaian listrik. Misalnya, persamaan kontinuitas mensyaratkan bahwa untuk setiap node (simpul dua atau lebih pipa), laju aliran bersih harus nol. Apa yang masuk ke suatu node harus keluar dengan laju yang sama. Selain itu, selisih tekanan bersih sepenuhnya di sekitar loop (dimulai dari satu lokasi dalam pipa dan kembali ke lokasi tersebut) harus nol. Dengan menggabungkan ide-ide ini dengan persamaan kehilangan head dan aliran pipa yang biasa, aliran di seluruh jaringan dapat ditentukan.

