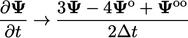Skema waktu orde kedua
Deret Taylor perluasan antara waktu sekarang 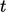 dan waktu ‘lama’ di berkaitan dengan skema implisit
dan waktu ‘lama’ di berkaitan dengan skema implisit 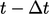 Euler oleh
Euler oleh
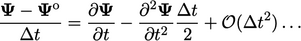 | (3.25) |
Kesalahan pemotongan 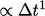 , yaitu akurasi orde pertama pada waktu ketika turunan waktu berhubungan dengan
, yaitu akurasi orde pertama pada waktu ketika turunan waktu berhubungan dengan 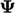 waktu saat ini , seperti yang ditunjukkan pada gambar di bawah ini. Meskipun orde rendah, skema Euler cukup akurat untuk banyak simulasi karena
waktu saat ini , seperti yang ditunjukkan pada gambar di bawah ini. Meskipun orde rendah, skema Euler cukup akurat untuk banyak simulasi karena 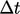 umumnya kecil jika sesuai dengan
umumnya kecil jika sesuai dengan 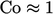 .
.
Namun demikian, skema waktu urutan kedua mungkin diperlukan untuk simulasi yang memerlukan akurasi temporal yang lebih tinggi atau untuk memungkinkan efisiensi komputasi yang lebih besar dengan menjalankannya dalam skala yang lebih besar 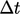 .
.
Skema Backward
Dalam Persamaan. (3.25) kita dapat menggantinya 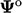 dengan nilai
dengan nilai 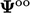 pada waktu ‘lama-lama’
pada waktu ‘lama-lama’ 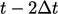 . Mengurangi ekspresi dari Persamaan. (3.25) dan penataan ulang suku-sukunya memberikan hubungan berikut untuk turunan kedua
. Mengurangi ekspresi dari Persamaan. (3.25) dan penataan ulang suku-sukunya memberikan hubungan berikut untuk turunan kedua
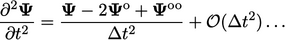 | (3.26) |
Skema Crank-Nicolson
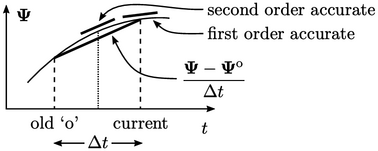
Sebuah implisitsolusi mengungkapkan istilah-istilah dalam suatu persamaan, misalnya adveksi, Laplacian, pada waktu saat ini . Metode Crank -Nicolson ,13 menyatakan istilah-istilah di titik tengah antara waktu sekarang dan waktu lama, untuk membuat skema waktu Euler orde kedua akurat. Dengan menyatakan suku-suku terdiskritisasi kecuali turunan waktu dengan 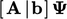 , metode Crank-Nicolson menyelesaikannya
, metode Crank-Nicolson menyelesaikannya
![@ 1 1 ---- + --[A jb ] + --[A jb ]o o = 0; @t Euler 2 2 \relax \special {t4ht=](https://doc.cfd.direct/notes/cfd-general-principles/img/index1359x.png) | (3.28) |
dimana 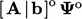 dihitung menggunakan nilai waktu lama
dihitung menggunakan nilai waktu lama 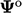 .
.
Versi modern dari skema ini menggantikan kedua 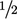 faktor tersebut dengan
faktor tersebut dengan 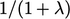 dan
dan 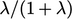 , memperkenalkan ‘koefisien offset’
, memperkenalkan ‘koefisien offset’ 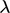 , yang
, yang 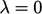 sesuai dengan implisit Euler dan
sesuai dengan implisit Euler dan 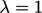 merupakan Persamaan Crank-Nicolson. (3.28). Jika
merupakan Persamaan Crank-Nicolson. (3.28). Jika 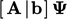 didiskritisasi secara implisit (seperti biasa), skema Crank-Nicolson dapat direpresentasikan sebagai turunan waktu yang didiskritisasi oleh
didiskritisasi secara implisit (seperti biasa), skema Crank-Nicolson dapat direpresentasikan sebagai turunan waktu yang didiskritisasi oleh
![@---- -------o o o @t ! (1 + ) t + [A jb] : \relax \special {t4ht=](https://doc.cfd.direct/notes/cfd-general-principles/img/index1369x.png) |
(3.29) |
Dalam praktiknya, 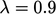 umumnya digunakan untuk memastikan stabilitas solusi.
umumnya digunakan untuk memastikan stabilitas solusi.

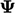 ,
, 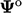 dan
dan 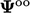 :
: