STEADY TWO DIMENSIONAL ADVECTION
Persamaan adveksi dua dimensi yang steady diberikan oleh:
Dengan mengintegrasikan atas elemen volume dua dimensi VC yang ditunjukkan dalam Gambar 11.16, menggunakan teorema divergensi, dan mengganti integral permukaan dengan penjumlahan atas wajah-wajah elemen, Persamaan (11.120) menjadi:

Gambar 11.16 Notasi untuk sistem grid Cartesius dua dimensi

Dengan menggunakan satu titik Gaussian untuk integral permukaan, sisi kiri dari Persamaan (11.121) diubah menjadi

Substitusi Persamaan (11.122) ke dalam Persamaan (11.121) menghasilkan
Bentuk diskritisasi penuh dari Persamaan (11.120) atas grid Kartesian diperoleh sebagai:

Dengan mengadopsi skema upwind dalam setiap arah koordinat dengan memperlakukan aliran sebagai lokal satu dimensi, Persamaan (11.124) menjadi:
dengan koefisien yang diberikan oleh
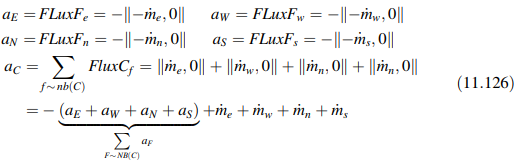
Jika skema QUICK digunakan, persamaan terdiskritisasi diubah menjadi
dengan koefisiennya dihitung sebagai
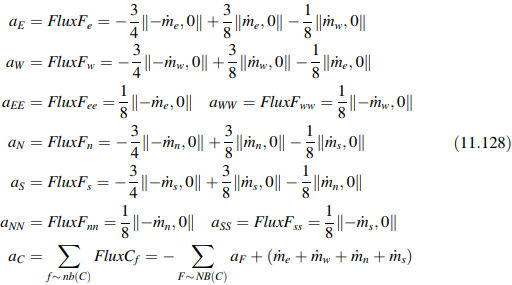
Kedua persamaan yang terdiskritisasi digunakan untuk memecahkan masalah adveksi murni dari profil langkah dalam medan kecepatan yang miring. Domain fisik secara skematis digambarkan dalam Gambar 11.17a. Ini mewakili domain persegi dengan properti ϕ yang diadveksi dalam medan dengan kecepatan v(1,1). Nilai dari ϕ adalah 1 di sisi kiri domain dan 0 di bagian bawah. Tanpa adanya difusi, solusi eksak adalah ϕ = 1 di atas diagonal yang ditunjukkan dalam Gambar 11.17a dan ϕ = 0 di bawahnya. Gambar 11.17b membandingkan profil eksak pada x = 0.5 dengan yang diperoleh secara numerik menggunakan skema upwind dan QUICK.

Gambar 11.17 a Domain fisik dan b Profil ϕ sepanjang garis tengah vertikal domain untuk adveksi murni dari profil langkah dalam medan kecepatan yang miring
Dibandingkan dengan solusi yang tepat, profil yang dihasilkan oleh skema upwind terbaur dan sangat tidak akurat tetapi sangat halus. Ketidakakuratan ini disebabkan oleh jenis kesalahan baru yang dikenal sebagai difusi lintang aliran, yang disebabkan oleh profil interpolasi satu dimensi yang digunakan, yaitu, ini disebabkan oleh perlakuan aliran sebagai lokal satu dimensi. Asal-usul difusi lintang aliran telah diidentifikasi oleh Patankar [4] dan Stubley [13] sebagai fenomena multidimensi. Ini terjadi hanya ketika medan kecepatan tidak sejajar dengan grid. Suatu ungkapan perkiraan untuk difusi aliran lintang telah diberikan oleh de Vahl Davis dan Mallinson [14] untuk aliran dua dimensi sebagai:
di mana ∣v∣ adalah magnitudo kecepatan dan θ adalah sudut yang dibuat oleh vektor kecepatan dengan sumbu koordinat x. Kesalahan ini dapat dikurangi dengan menggunakan skema interpolasi orde yang lebih tinggi seperti yang ditunjukkan oleh profil yang dihasilkan dengan skema QUICK. Profil skema QUICK terbukti jauh lebih tajam dan lebih akurat daripada profil upwind namun terinfeksi dengan overshoots/devershoots di dekat gradien tajam. Seperti yang disebutkan sebelumnya, kesalahan ini disebut kesalahan dispersi, yang menyebabkan pembentukan maksima/minima di domain solusi dan merupakan karakteristik dari semua skema High Order (HO).
