SUKU LAINNYA
Dalam suatu persamaan untuk 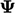 , bisa ada suku-suku selain turunan waktu, adveksi, dan Laplasian dari
, bisa ada suku-suku selain turunan waktu, adveksi, dan Laplasian dari 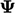 , termasuk:
, termasuk:
- Fungsi linear
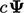 di mana
di mana  adalah suku-suku skalar atau lapangan
adalah suku-suku skalar atau lapangan - Suatu suku tanpa
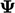 , terkadang termasuk turunan variabel lain, misalnya
, terkadang termasuk turunan variabel lain, misalnya 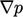 .
.
Contoh kedua ini hanya diskritisasi sebagai suatu suku gradien eksplisit seperti yang dijelaskan dalam Bagian 3.15. Suku-suku turunan seperti contoh ini telah dijelaskan di bagian sebelumnya dan tidak memerlukan diskusi lebih lanjut.
Contoh pertama, istilah 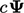 , memerlukan pembahasan lebih lanjut, terutama terkait kemungkinan diskritisasi implisit. Mari kita pertimbangkan persamaan berikut :
, memerlukan pembahasan lebih lanjut, terutama terkait kemungkinan diskritisasi implisit. Mari kita pertimbangkan persamaan berikut :
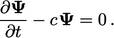 | (3.33) |
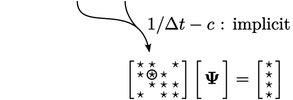
Jika 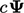 terdiskritisasi secara implisit, maka matriks akan mengandung koefisien digaonal nol saat
terdiskritisasi secara implisit, maka matriks akan mengandung koefisien digaonal nol saat 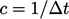 , menjadikannya singular atau tidak dapat diinvers. Jika ini terjadi,
, menjadikannya singular atau tidak dapat diinvers. Jika ini terjadi, 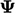 tidak hadir dalam persamaan linear untuk sel yang relevan, sehingga tidak dapat dipecahkan.
tidak hadir dalam persamaan linear untuk sel yang relevan, sehingga tidak dapat dipecahkan.
Oleh karena itu, suatu suku haruus terdiskritisasi secara eksplisit ketika memiliki tanda negatif (atau positif di sebelah kanan “=”), untuk memastikan persamaan matriks dapat dipecahkan. Sifat dari pers. (3.33) adalah bahwa 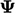 hanya dapat meningkat dari nilai positif awal.
hanya dapat meningkat dari nilai positif awal.
Diskritisasi Implisit Suku Linear
Sekarang mari kita pertimbangkan persamaan yang setara dengan suku linear yang memiliki tanda positif, yaitu
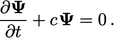 | (3.34) |
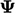 hanya dapat berkurang dari nilai positif awal tetapi mencapai batas rendah pada
hanya dapat berkurang dari nilai positif awal tetapi mencapai batas rendah pada 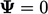 . Seperti banyak properti skalar, misalnya
. Seperti banyak properti skalar, misalnya 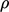 ,
, 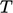 ,
,  , dll.,
, dll., 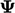 mungkin memiliki batas fisik bawah 0, yang sengaja tercermin dalam persamaan.
mungkin memiliki batas fisik bawah 0, yang sengaja tercermin dalam persamaan.
Penting untuk mempertahankan batas fisik dari persamaan 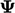 . Diskritisasi (3.34) menggunakan skema waktu Euler (3.21) memberikan
. Diskritisasi (3.34) menggunakan skema waktu Euler (3.21) memberikan
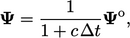 | (3.35) |
yang menjamin batasan sejak itu 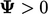 . Diskritisasi eksplisit yang setara memberikan
. Diskritisasi eksplisit yang setara memberikan 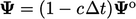 yang hanya dibatasi ketika
yang hanya dibatasi ketika 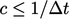 , serupa dengan
, serupa dengan 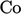 batas yang ditentukan oleh diskritisasi adveksi eksplisit, yang dijelaskan dalam Bagian. 3.17. Untuk menghindari
batas yang ditentukan oleh diskritisasi adveksi eksplisit, yang dijelaskan dalam Bagian. 3.17. Untuk menghindari 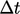 batasan ini, kami menerapkan diskritisasi implisit pada suku-suku dengan tanda positif di sisi kiri “=”, jika memungkinkan. Meskipun suku tersebut tidak linier
batasan ini, kami menerapkan diskritisasi implisit pada suku-suku dengan tanda positif di sisi kiri “=”, jika memungkinkan. Meskipun suku tersebut tidak linier 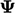 , suku tersebut dapat diterapkan dengan “membagi dan mengalikan dengan
, suku tersebut dapat diterapkan dengan “membagi dan mengalikan dengan 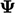 ”. Misalnya,
”. Misalnya,  model turbulensi memasukkan suatu
model turbulensi memasukkan suatu 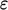 suku ke dalam
suku ke dalam 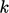 persamaan, yaitu
persamaan, yaitu 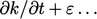 mengabaikan suku lainnya. Membagi dan mengalikan
mengabaikan suku lainnya. Membagi dan mengalikan 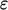 suku dengan
suku dengan 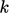 memberi
memberi
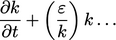 |
(3.36) |
menghasilkan suku linier yang 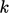 dapat didiskritisasi secara implisit menggunakan koefisien
dapat didiskritisasi secara implisit menggunakan koefisien 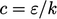 .
.
