Sumber dalam Aliran Seragam—Setengah Tubuh
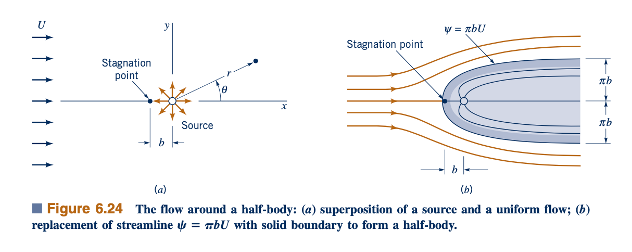
Pertimbangkan superposisi sebuah sumber dan aliran seragam seperti yang ditunjukkan dalam Gambar 6.24a. Fungsi arus yang dihasilkan adalah:
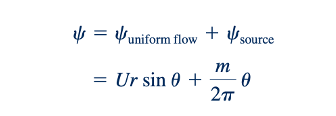
dan potensial kecepatan yang sesuai adalah:

Jelas bahwa di beberapa titik di sepanjang sumbu x negatif, kecepatan akibat sumber akan hanya membatalkan kecepatan akibat aliran seragam dan titik stagnasi akan terbentuk. Untuk sumber saja

sehingga titik stagnasi akan terjadi pada x = −b, di mana
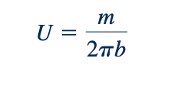
Atau

Nilai fungsi aliran di titik stagnasi dapat diperoleh dengan mengevaluasi 𝜓 pada r = b dan 𝜃 = 𝜋, yang menghasilkan dari Persamaan 6.97:

Karena m2 = 𝜋 b U (dari Persamaan 6.99), maka persamaan garis aliran yang melalui titik stagnasi adalah
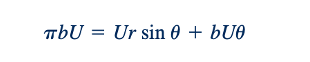
Atau

dimana 𝜃 dapat bervariasi antara 0 dan 2π. Plot dari garis aliran ini ditunjukkan dalam Gambar 6.24b. Jika kita menggantikan garis aliran ini dengan batas padat, seperti yang ditunjukkan dalam gambar, maka jelas bahwa kombinasi aliran seragam dan sumber ini dapat digunakan untuk menjelaskan aliran di sekitar sebuah tubuh berstreamline yang ditempatkan dalam aliran seragam. Tubuh ini terbuka di ujung hilir dan oleh karena itu disebut sebagai separuh tubuh. Garis aliran lain dalam medan aliran dapat diperoleh dengan menetapkan 𝜓 = konstan dalam Persamaan 6.97 dan memplot persamaan yang dihasilkan. Sejumlah garis aliran ini ditunjukkan dalam Gambar 6.24b. Meskipun garis-garis aliran di dalam tubuh ditunjukkan, sebenarnya mereka tidak menarik dalam kasus ini, karena kita hanya peduli dengan medan aliran di luar tubuh. Perlu dicatat bahwa singularitas dalam medan aliran (sumber) terjadi di dalam tubuh, dan tidak ada singularitas dalam medan aliran yang menarik (di luar tubuh).
Lebar separuh tubuh mendekati secara asimtotik 2𝜋b= m/U . Dengan demikian, seperti yang ditunjukkan oleh gambar di pinggiran, untuk kecepatan aliran bebas U yang diberikan, lebar separuh tubuh meningkat seiring dengan kekuatan sumber. Hal ini mengikuti dari Persamaan 6.100, yang dapat ditulis sebagai:

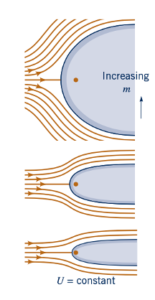
sehingga saat 𝜃→0 atau 𝜃→2π, separuh lebar mendekati b. Dengan fungsi aliran (atau potensial kecepatan) diketahui, komponen kecepatan di setiap titik dapat diperoleh. Untuk separuh tubuh, dengan menggunakan fungsi aliran yang diberikan oleh Persamaan 6.97,

dan

Oleh karena itu, kuadrat magnitudo kecepatan, V, di setiap titik adalah:
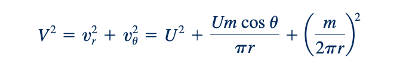
dan karena b= m/2πU

Dengan kecepatan diketahui, tekanan di setiap titik dapat ditentukan dari persamaan Bernoulli, yang dapat dituliskan antara dua titik mana pun dalam medan aliran karena aliran bersifat irrotasional. Dengan demikian, menerapkan persamaan Bernoulli antara sebuah titik jauh dari tubuh, di mana tekanannya p0 dan kecepatannya U, dan sebuah titik sembarang dengan tekanan p dan kecepatan V, maka diperoleh bahwa:
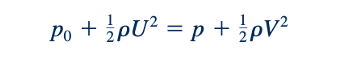
di mana perubahan elevasi diabaikan. Persamaan 6.101 sekarang dapat digunakan dalam Persamaan 6.102 untuk mendapatkan tekanan di setiap titik dalam hal tekanan referensi, p0 , dan kecepatan aliran hulu, U.
Aliran potensial ini yang relatif sederhana memberikan beberapa informasi berguna tentang aliran di sekitar bagian depan dari sebuah tubuh berstreamline, seperti penopang jembatan atau angkur yang ditempatkan dalam aliran seragam. Sebuah titik penting yang perlu diperhatikan adalah bahwa kecepatan tangensial terhadap permukaan tubuh tidak nol; artinya, fluida "meluncur" melewati batas. Hasil ini adalah konsekuensi dari mengabaikan viskositas, sifat fluida yang menyebabkan fluida nyata menempel pada batas, sehingga menciptakan kondisi "no-slip". Semua aliran potensial berbeda dari aliran fluida nyata dalam hal ini dan tidak secara akurat mewakili kecepatan sangat dekat dengan batas. Namun, di luar lapisan batas yang sangat tipis ini, distribusi kecepatan umumnya akan sesuai dengan yang diprediksi oleh teori aliran potensial jika tidak terjadi pemisahan aliran. Lihat Bagian 9.2.6.2. Selain itu, distribusi tekanan sepanjang permukaan akan sangat mendekati yang diprediksi dari teori aliran potensial, karena lapisan batas tipis dan tidak ada kesempatan bagi tekanan untuk bervariasi melalui lapisan tipis tersebut. Bahkan, seperti yang dibahas lebih detail dalam Bab 9, distribusi tekanan yang diperoleh dari teori aliran potensial digunakan bersama dengan teori aliran viskos untuk menentukan sifat aliran dalam lapisan batas.