4.12 Symmetry Condition

4.12 symmetry condition

Kondisi batas transformasi disajikan pada Sec. 4.11. Ini memberikan kerangka kerja yang mudah untuk menerapkan kondisi batas yang mewakili batasan geometris , termasuk kondisi simetri .

Kondisi simetri cocok untuk simulasi dimana geometrinya mengandung bidang simetri dan medan aliran diasumsikan simetris. Dengan menghasilkan mesh pada satu sisi bidang simetri dan menerapkan kondisi simetri, jumlah sel, dan waktu penyelesaian, berkurang.

Dalam konteks batas dinding, kondisi simetri juga setara dengan slip (berbeda dengan kondisi no-slip pada umumnya).

Bidang simetri merupakan kondisi transformasi sehingga jika variabel solusinya 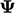$persamaan$ berupa skalar, maka gradiennya akan berkurang menjadi nol. Untuk suatu vektor, misalnya 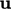$persamaan$ , kondisinya adalah gradien nol yang bersinggungan dengan bidang, dan nilai nol tetap normal terhadap bidang.

Jika 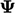$persamaan$ merupakan tensor, kondisi batas memerlukan definisi yang lebih tepat, yang juga dapat diterapkan pada vektor 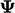$persamaan$ . Batas 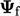$persamaan$ dapat dianggap sebagai rata-rata sel yang berdekatan 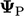$persamaan$ dan bayangan cermin 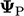$persamaan$ yang ditransformasikan oleh tensor transformasi reflektif 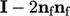$persamaan$ , yaitu

Di sini, 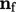$persamaan$ adalah vektor normal satuan pada permukaan batas.

Menggunakan notasi di Sec. 4.11, nilai batas eksplisit 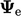$persamaan$ dihitung menggunakan arus 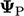$persamaan$ dari Persamaan. (4.18) dan gradien eksplisit 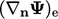$persamaan$ dihitung dengan Persamaan. (4.17).

Membandingkan Persamaan. (4.18) dengan kondisi transformasi Sec. 4.11, faktornya 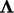$persamaan$ sesuai dengan tensor 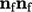$persamaan$ . Untuk bidang vektor, faktor yang memberikan konvergensi solusi yang baik adalah

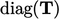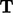dimana “ $persamaan$ ” adalah vektor komponen diagonal tensor $persamaan$ .

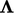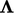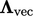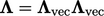Untuk bidang tensor, konvergensi yang baik dicapai dengan tensor $persamaan$ yang dihitung sebagai hasil kali luar dari $persamaan$ sebuah vektor, yaitu dengan menyatakan faktor vektor dengan $persamaan$ , maka faktor tensornya adalah $persamaan$ .

Kondisi ortogonalitas

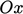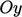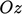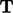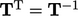Sumbu $persamaan$ , $persamaan$ , $persamaan$ , diperkenalkan di Sec. 2.1, harus tetap ortogonal dalam transformasi. Hal ini memerlukan transpos tensor transformasi $persamaan$ agar sama dengan inversnya, yaitu $persamaan$ .

Oleh karena itu, kondisi ortogonalitasnya adalah 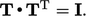$persamaan$ Transformasi reflektif $persamaan$ memenuhi kondisi ortogonalitas sejak saat itu