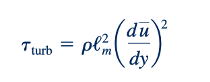Tegangan Geser Turbulen
Perbedaan mendasar antara aliran laminar dan turbulen terletak pada perilaku kacau dan acak dari berbagai parameter fluida. Variasi semacam itu terjadi dalam tiga komponen kecepatan, tekanan, tegangan geser, suhu, dan variabel lain yang memiliki deskripsi lapangan. Aliran turbulen ditandai oleh vortisitas tiga dimensi yang acak (misalnya, rotasi atau putaran partikel fluida; lihat Bagian 6.1.3). Seperti yang ditunjukkan dalam Gambar 8.12, aliran tersebut dapat dijelaskan dalam istilah nilai rata-rata mereka (ditandai dengan garis overbar) yang ditambahkan dengan fluktuasi (ditandai dengan tanda primer). Dengan demikian, jika u adalah komponen x dari kecepatan instan, maka nilai rata-rata waktu (atau rata-rata waktu) nya, u, atau u = (x,y,z,t) adalah
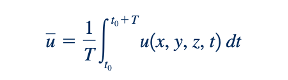
di mana interval waktu, T, jauh lebih lama dari periode fluktuasi terpanjang, tetapi jauh lebih pendek dari ketidakmantapan kecepatan rata-rata yang ada. Ini diilustrasikan dalam Gambar 8.12.
Bagian yang fluktuatif dari kecepatan, u', adalah bagian yang berubah seiring waktu yang berbeda dari nilai rata-rata.
Jelas, rerata waktu dari fluktuasi adalah nol, karena
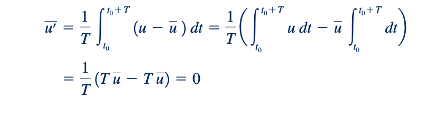

Fluktuasi terdistribusi secara merata di kedua sisi dari rerata. Juga jelas, seperti yang ditunjukkan dalam Gambar 8.13, bahwa karena kuadrat dari sebuah variabel fluktuasi tidak dapat menjadi negatif [(u')² ≥ 0], maka nilai reratanya adalah positif. Oleh karena itu,
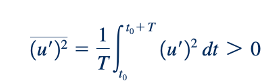
Di sisi lain, mungkin bahwa rerata dari produk-produk fluktuasi, seperti u'v', adalah nol atau bukan nol (baik positif maupun negatif).
Struktur dan karakteristik turbulensi dapat bervariasi dari satu situasi aliran ke situasi aliran lainnya. Sebagai contoh, intensitas turbulensi (atau tingkat turbulensi) mungkin lebih besar dalam angin yang sangat berhembus daripada dalam angin yang relatif stabil (meskipun tetap turbulen). Intensitas turbulensi, i, sering didefinisikan sebagai akar kuadrat dari rerata kuadrat dari kecepatan fluktuasi dibagi oleh kecepatan rerata dalam waktu, atau
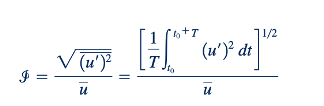

Semakin besar intensitas turbulensi, semakin besar fluktuasi kecepatan (dan parameter aliran lainnya). Terowongan angin yang dirancang dengan baik memiliki nilai ℐ≈ khas sekitar 0,01, meskipun dengan perawatan ekstrem, nilai serendah ℐ 0,0002 telah diperoleh. Di sisi lain, nilai ℐ≥ 0,1 ditemukan untuk aliran di atmosfer dan sungai. Grafik kecepatan angin atmosfer tipikal ditunjukkan dalam gambar di margin.
Parameter turbulensi lain yang berbeda dari satu situasi aliran ke situasi lainnya adalah periode fluktuasi — skala waktu fluktuasi yang ditunjukkan dalam Gambar 8.12. Dalam banyak aliran, seperti aliran air dari keran, frekuensi khas berada dalam kisaran 10, 100, atau 1000 siklus per detik (cps). Untuk aliran lain, seperti arus Gulf Stream di Samudra Atlantik atau aliran atmosfer di Jupiter, osilasi acak karakteristik mungkin memiliki periode dalam hitungan jam, hari, atau lebih.
Menggoda untuk memperluas konsep tegangan geser viskos untuk aliran laminar (𝜏=𝜇𝑑𝑢/𝑑𝑦) ke aliran turbulen dengan mengganti u, kecepatan instan, dengan u, kecepatan rata-rata waktu. Namun, banyak studi eksperimental dan teoritis telah menunjukkan bahwa pendekatan seperti ini menghasilkan hasil yang sama sekali tidak benar. Artinya, 𝜏≠𝜇 𝑑 𝑢/𝑑𝑦. Penjelasan fisik untuk perilaku ini dapat ditemukan dalam konsep apa yang menghasilkan tegangan geser.
Aliran laminar dimodelkan sebagai partikel fluida yang mengalir dengan lancar di dalam lapisan, meluncur melewati yang sedikit lebih lambat atau lebih cepat di sisi-sisinya. Seperti yang dibahas dalam Bab 1, fluida sebenarnya terdiri dari banyak molekul yang bergerak dengan cara yang hampir acak seperti yang ditunjukkan dalam Gambar 8.14a. Gerakan ini tidak sepenuhnya acak — kecenderungan kecil ke satu arah menghasilkan laju aliran yang kita asosiasikan
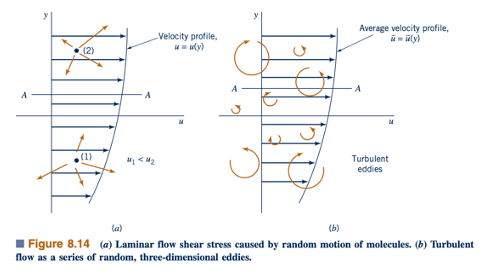
Sarang partikel fluida, u. Ketika molekul melintasi suatu bidang tertentu (misalnya bidang A - A), mereka yang bergerak ke atas berasal dari daerah dengan rata-rata komponen kecepatan x yang lebih kecil daripada mereka yang bergerak ke bawah, yang berasal dari daerah dengan kecepatan yang lebih besar.
Fluks momentum dalam arah x melintasi bidang A - A menyebabkan gaya geser (ke kiri) dari fluida bagian bawah pada fluida bagian atas dan efek yang sama namun berlawanan dari fluida bagian atas pada fluida bagian bawah. Molekul-molekul yang lamban bergerak ke atas melintasi bidang A - A harus dipercepat oleh fluida di atas bidang ini. Perubahan momentum dalam proses ini menghasilkan gaya geser (dalam skala makroskopis). Begitu pula, molekul-molekul yang lebih energik yang bergerak ke bawah melintasi bidang A - A harus diperlambat oleh fluida di bawah bidang tersebut. Gaya geser ini hadir hanya jika ada gradien dalam u 1y2, jika tidak, komponen kecepatan x (dan momentum) rata-rata dari molekul yang bergerak ke atas dan ke bawah akan sama persis. Selain itu, terdapat gaya tarik-menarik antara molekul-molekul tersebut. Dengan menggabungkan efek-efek ini, kita mendapatkan hukum viskositas Newton yang terkenal: 𝜏=𝜇𝑑𝑢/𝑑𝑦, di mana dalam basis molekuler, m berkaitan dengan massa dan kecepatan (suhu) gerak acak molekul.
Meskipun gerak acak molekul seperti di atas juga ada dalam aliran turbulen, ada faktor lain yang umumnya lebih penting. Cara yang sederhana untuk memikirkan tentang aliran turbulen adalah dengan menganggapnya terdiri dari serangkaian gerakan eddy tiga dimensi yang acak seperti yang digambarkan (dalam satu dimensi saja) dalam Gambar 8.14b. (Lihat foto di awal bab ini.) Eddy ini bervariasi dalam ukuran dari diameter sangat kecil (sekitar ukuran partikel fluida) hingga diameter yang cukup besar (sekitar ukuran objek atau geometri aliran yang dipertimbangkan). Mereka bergerak secara acak, membawa massa dengan kecepatan rata-rata u= u (y). Struktur eddy ini sangat meningkatkan pencampuran dalam fluida. Ini juga sangat meningkatkan transportasi momentum x melintasi bidang A - A. Itu adalah partikel-fluida terbatas (bukan hanya molekul individu seperti dalam aliran laminar) yang secara acak diangkut melintasi bidang ini, menghasilkan gaya geser yang relatif besar (dibandingkan dengan aliran laminar). Partikel-partikel ini bervariasi dalam ukuran tetapi jauh lebih besar dari molekul.
Komponen kecepatan acak yang menyebabkan transfer momentum ini (oleh karena itu, gaya geser) adalah u' (untuk komponen kecepatan x) dan v' (untuk laju transfer massa yang melintasi bidang). Pertimbangan yang lebih rinci tentang proses yang terlibat akan menunjukkan bahwa tegangan geser yang tampak pada bidang A - A diberikan oleh persamaan berikut (Ref. 22):

Perhatikan bahwa jika aliran adalah laminar, u'= v' = 0, sehingga u'v' = 0 dan Persamaan 8.26 menyederhanakan menjadi tegangan geser laminar yang disebabkan oleh gerakan acak molekul, 𝜏𝑙𝑎𝑚= 𝜇 𝑑 𝑢/𝑑𝑦. Untuk aliran turbulen ditemukan bahwa tegangan geser turbulen, 𝜏 𝑡𝑢𝑟𝑏=−𝑝𝑢^′ 𝑣′, adalah positif. Oleh karena itu, tegangan geser lebih besar dalam aliran turbulen daripada dalam aliran laminar. Perhatikan satuan pada 𝜏 𝑡𝑢𝑟𝑏 adalah (massa jenis)( (kecepatan)2 =, yang dalam satuan turun (slug-ft/s3) (ft/s)2 = (slug . ft/s2)/ft2 = Ib/ft2, atau N/m2, seperti yang diharapkan. Istilah yang mengandung -ρu'v' (atau -ρv'w', dll.) disebut tegangan Reynolds untuk menghormati Osborne Reynolds yang pertama kali membahasnya pada tahun 1895.
Dari Persamaan 8.26, terlihat bahwa tegangan geser dalam aliran turbulen tidak hanya
berbanding lurus dengan gradien dari kecepatan rata-rata waktu, u(y). Ini juga mengandung kontribusi karena fluktuasi acak dari komponen x dan y kecepatan. Kerapatan terlibat karena transfer momentum dari fluida dalam pusaran acak. Meskipun magnitudo relatif dari 𝜏 𝑙𝑎𝑚 mungkin menunjukkan struktur yang ditunjukkan dalam Fig. 8.15a. (Ingat dari Persamaan 8.4 bahwa tegangan geser berkaitan dengan jarak dari garis tengah pipa). Dalam daerah yang sangat sempit dekat dinding (lapisan subviskos), tegangan geser laminar mendominasi. Jauh dari dinding (lapisan luar), bagian turbulen dari tegangan geser mendominasi. Transisi antara kedua daerah ini terjadi di lapisan tumpang tindih. Profil kecepatan khas yang sesuai ditunjukkan dalam Fig. 8.15b.
Skala gambar yang ditunjukkan dalam Fig. 8.15 tidak selalu benar. Biasanya nilai 𝜏 𝑡𝑢𝑟𝑏 sekitar 100 hingga 1000 kali lebih besar dari 𝜏 𝑙𝑎𝑚 di daerah luar, sementara sebaliknya terjadi di lapisan subviskos. Pemodelan yang benar dari aliran turbulen sangat bergantung pada pengetahuan yang akurat mengenai properti aliran turbulen. Skala vertikal dari Fig. 8.15 juga distorsi. Lapisan subviskos biasanya merupakan lapisan yang sangat tipis yang berdekatan dengan dinding. Misalnya, untuk aliran air dalam pipa berdiameter 3 inci dengan kecepatan rata-rata 10 ft/s, lapisan subviskosnya kira-kira tebal 0.002 inci. Karena gerakan fluida dalam lapisan tipis ini kritis dalam hal aliran secara keseluruhan (kondisi no-slip dan tegangan geser dinding terjadi dalam lapisan ini), tidak mengherankan menemukan bahwa properti aliran pipa turbulen dapat cukup dibandingkan dengan 𝜏 𝑡𝑢𝑟𝑏 adalah fungsi kompleks yang tergantung pada aliran tertentu yang terlibat, pengukuran khas turb menunjukkan struktur yang ditunjukkan dalam Fig. 8.15a. (Ingat dari Persamaan 8.4 bahwa tegangan geser berkaitan dengan jarak dari garis tengah pipa). Dalam daerah yang sangat sempit dekat dinding (lapisan subviskos), tegangan geser laminar mendominasi. Jauh dari dinding (lapisan luar), bagian turbulen dari tegangan geser mendominasi. Transisi antara kedua daerah ini terjadi di lapisan tumpang tindih. Profil kecepatan khas yang sesuai ditunjukkan dalam Fig. 8.15b.
Namun, belum mungkin untuk memecahkan persamaan-persamaan yang mengatur (persamaan Navier-Stokes) untuk detail-detail aliran ini, meskipun teknik-teknik numerik yang menggunakan komputer terbesar dan tercepat yang tersedia telah menghasilkan informasi penting tentang beberapa karakteristik turbulensi. Upaya besar telah dilakukan dalam studi tentang turbulensi. Banyak yang masih perlu dipelajari. Mungkin studi di bidang baru tentang kekacauan dan geometri fraktal akan memberikan alat untuk pemahaman yang lebih baik tentang turbulensi.

bergantung pada kasar permukaan dinding pipa, berbeda dengan aliran pipa laminar yang tidak bergantung pada kasar permukaan. Elemen kasar kecil seperti goresan, karat, pasir, atau partikel kotoran dapat dengan mudah mengganggu lapisan subviskositas ini, sehingga memengaruhi seluruh aliran.
Bentuk alternatif untuk tegangan geser aliran turbulen diberikan dalam bentuk viskositas pusaran, 𝜂 , di mana

Pengembangan terminologi aliran laminar ini diperkenalkan oleh J. Boussinesq, seorang ilmuwan Prancis, pada tahun 1877. Meskipun konsep viskositas pusaran menarik, dalam praktiknya ini bukan parameter yang mudah digunakan. Berbeda dengan viskositas mutlak, μ, yang merupakan nilai yang diketahui untuk fluida tertentu, viskositas pusaran adalah fungsi baik dari fluida maupun kondisi aliran. Artinya, viskositas pusaran air tidak dapat dilihat di buku panduan—nilainya berubah dari satu kondisi aliran turbulen ke kondisi yang lain dan dari satu titik dalam aliran turbulen ke titik yang lain.
Ketidak mampuan untuk secara akurat menentukan tekanan Reynolds, ‾ρu′ v' , setara dengan tidak mengetahui viskositas pusaran. Beberapa teori semi-empiris telah diusulkan untuk menentukan nilai perkiraan dari 𝜂.L. Prandtl (1875–1953), seorang fisikawan dan ahli aerodinamika Jerman, mengusulkan bahwa proses turbulen bisa dilihat sebagai transportasi acak bundel partikel fluida selama suatu jarak, ℓ𝑚, panjang campuran, dari suatu wilayah satu kecepatan ke wilayah lain dengan kecepatan yang berbeda. Dengan menggunakan beberapa asumsi ad hoc dan penalaran fisik, disimpulkan bahwa viskositas pusaran diberikan oleh
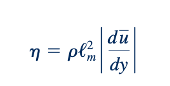
Oleh karena itu, tegangan geser turbulen adalah