Tekanan pada Suatu Titik
Seperti yang dibahas singkat di Bab 1, istilah tekanan digunakan untuk menunjukkan gaya normal per satuan luas pada titik tertentu yang bertindak pada bidang tertentu dalam massa fluida yang diminati. Pertanyaan yang muncul secara langsung adalah bagaimana tekanan pada suatu titik bervariasi dengan orientasi bidang yang melewati titik tersebut. Untuk menjawab pertanyaan ini, pertimbangkan diagram benda bebas, yang diilustrasikan dalam Gambar 2.1.

Hal itu diperoleh dengan menghilangkan segmen kecil segitiga fluida dari lokasi sembarang dalam suatu massa fluida. Karena kita sedang mempertimbangkan situasi di mana tidak ada gaya geser, satu-satunya gaya eksternal yang bertindak pada segmen adalah karena tekanan dan berat. Untuk kesederhanaan, gaya dalam arah x tidak ditampilkan, dan sumbu z diambil sebagai sumbu vertikal sehingga berat bertindak dalam arah z negatif. Meskipun kita terutama tertarik pada fluida dalam keadaan diam, untuk membuat analisis seumum mungkin, kita akan memungkinkan unsur fluida memiliki gerakan yang dipercepat. Asumsi tentang nol gaya geser masih akan berlaku selama unsur fluida bergerak sebagai benda kaku; artinya, tidak ada gerakan relatif antara elemen-elemen yang berdekatan.
Persamaan gerak (Hukum kedua Newton, F = ma) dalam arah y dan z adalah, secara berurutan,
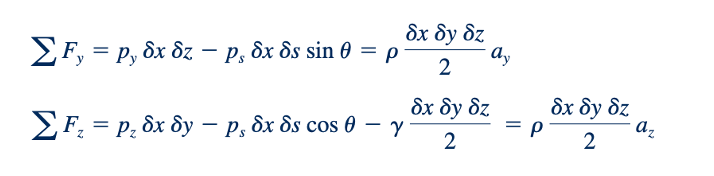
di mana ps, py, dan pz adalah tekanan rata-rata pada permukaan, 𝛾 dan 𝜌 adalah berat jenis dan densitas fluida, secara berturut-turut, dan ay, az adalah percepatan. Perlu diperhatikan bahwa tekanan harus dikalikan dengan luas yang sesuai untuk mendapatkan gaya yang dihasilkan oleh tekanan. Dari geometri, dapat disimpulkan bahwa

sehingga persamaan gerak dapat dituliskan ulang sebagai:

Karena kita benar-benar tertarik pada apa yang terjadi di suatu titik, kita mengambil batas saat dx, dy, dan dz mendekati nol (sementara mempertahankan sudut θ), dan itu mengikuti bahwa:

atau ps = py = pz. Sudut θ dipilih secara sembarangan sehingga kita dapat menyimpulkan bahwa tekanan pada suatu titik dalam fluida yang diam, atau dalam gerakan, tidak tergantung pada arah selama tidak ada tegangan geser yang hadir. Hasil penting ini dikenal sebagai hukum Pascal, dinamai sesuai dengan Blaise Pascal 11623–16622, seorang matematikawan Prancis yang membuat kontribusi penting dalam bidang hidrostatika. Dengan demikian, seperti yang ditunjukkan oleh fotografi di sisi margin, di perempatan sisi dan dasar beaker, tekanannya sama di sisi dan dasar. Pada Bab 6 akan diperlihatkan bahwa untuk fluida yang bergerak di mana ada gerakan relatif antara partikel (sehingga tegangan geser berkembang), tegangan normal pada suatu titik, yang sesuai dengan tekanan dalam fluida diam, tidak selalu sama dalam semua arah. Dalam kasus seperti itu, tekanan didefinisikan sebagai rata-rata dari tiga tegangan normal saling tegak lurus di titik tersebut.

