
Teori Model
Teori model dapat dengan mudah dikembangkan dengan menggunakan prinsip analisis dimensional. Telah ditunjukkan bahwa setiap masalah tertentu dapat dijelaskan dalam bentuk serangkaian pi term sebagai
Dalam merumuskan hubungan ini, hanya pengetahuan tentang sifat umum fenomena fisik, dan variabel yang terlibat, yang diperlukan. Nilai-nilai spesifik untuk variabel (ukuran komponen, properti fluida, dll.) tidak diperlukan untuk melakukan analisis dimensional. Dengan demikian, persamaan 7.7 berlaku untuk setiap sistem yang diatur oleh variabel yang sama. Jika Persamaan 7.7 menggambarkan perilaku prototipe tertentu, hubungan serupa dapat ditulis untuk sebuah model dari prototipe ini; yaitu,
dimana bentuk fungsi akan sama selama fenomena yang sama terlibat dalam kedua prototipe dan model. Variabel, atau pi term, tanpa subskrip akan mengacu pada prototipe, sedangkan subskrip m akan digunakan untuk menunjukkan variabel atau pi term model.
Pi term dapat dikembangkan sehingga Π1 mengandung variabel yang akan diprediksi dari pengamatan yang dilakukan pada model. Oleh karena itu, jika model dirancang dan dioperasikan di bawah kondisi berikut,

maka dengan asumsi bahwa bentuk 𝜙 sama untuk model dan prototipe, maka

Persamaan 7.10 adalah persamaan prediksi yang diinginkan dan menunjukkan bahwa nilai yang diukur dari Π1m yang diperoleh dengan model akan sama dengan Π1 yang sesuai untuk prototipe selama pi term lainnya sama. Kondisi yang ditentukan oleh Persamaan 7.9 menyediakan kondisi desain model, juga disebut persyaratan kesamaan atau hukum pemodelan.
Sebagai contoh dari prosedur tersebut, pertimbangkan masalah penentuan gaya tarik, 𝔇, pada sebuah pelat persegi panjang tipis (w x h) yang ditempatkan tegak lurus terhadap fluida dengan kecepatan V, seperti yang ditunjukkan oleh gambar di margin. Analisis dimensional dari masalah ini dilakukan dalam Contoh 7.1, di mana diasumsikan bahwa

Penerapan
Penerapan teorema pi menghasilkan


Kita sekarang tertarik untuk merancang sebuah model yang dapat digunakan untuk memprediksi gaya tarik pada suatu prototipe tertentu (yang kemungkinan memiliki ukuran yang berbeda dengan model). Karena hubungan yang dinyatakan oleh Persamaan 7.11 berlaku baik untuk prototipe maupun model, diasumsikan bahwa Persamaan 7.11 mengatur prototipe, dengan hubungan yang serupa

untuk model. Kondisi desain model, atau persyaratan kesamaan, oleh karena itu

Ukuran model diperoleh dari persyaratan pertama yang mengindikasikan bahwa
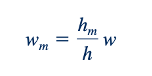
Kita bebas menetapkan rasio tinggi antara model dan prototipe, hm/h, tetapi kemudian lebar pelat model, wm, ditetapkan sesuai dengan Persamaan 7.13.
Persyaratan kesamaan kedua mengindikasikan bahwa model dan prototipe harus dioperasikan pada nomor Reynolds yang sama. Dengan demikian, kecepatan yang diperlukan untuk model diperoleh dari hubungan

Perhatikan bahwa desain model ini memerlukan tidak hanya penskalaan geometris, seperti yang ditentukan oleh Persamaan 7.13, tetapi juga penskalaan kecepatan yang benar sesuai dengan Persamaan 7.14. Hasil ini adalah tipikal dari sebagian besar desain model – ada lebih dari sekadar penskalaan geometri!
Dengan persyaratan kesamaan yang telah disebutkan terpenuhi, persamaan prediksi untuk gaya tarik adalah

Atau

Dengan demikian, gaya tarik yang diukur pada model, 𝔇m, harus dikalikan dengan rasio kuadrat lebar pelat, rasio densitas fluida, dan rasio kuadrat kecepatan untuk mendapatkan nilai prediksi gaya tarik prototipe, 𝔇.
Kesimpulan
Secara umum, seperti yang diilustrasikan dalam contoh ini, untuk mencapai kesamaan perilaku antara model dan prototipe, semua pi term yang sesuai harus disejajarkan antara model dan prototipe. Biasanya, satu atau lebih dari pi term ini akan melibatkan rasio panjang penting (seperti w × h dalam contoh sebelumnya); yaitu, mereka bersifat murni geometris. Oleh karena itu, ketika kita menyamakan pi term yang melibatkan rasio panjang, kita mengharuskan adanya kesamaan geometris lengkap antara model dan prototipe. Ini berarti bahwa model harus merupakan versi yang diperbesar dari prototipe. Penskalaan geometris dapat mencakup fitur terkecil dari sistem, seperti kekasaran permukaan, atau tonjolan kecil pada sebuah struktur, karena jenis fitur geometris ini dapat secara signifikan mempengaruhi aliran. Setiap penyimpangan dari kesamaan geometris lengkap untuk sebuah model harus dipertimbangkan dengan hati-hati. Terkadang penskalaan geometris lengkap mungkin sulit untuk dicapai, terutama ketika berurusan dengan kekasaran permukaan, karena kekasaran sulit untuk dikarakterisasi dan dikendalikan.
Sebuah kelompok pi term tipikal lainnya (seperti nomor Reynolds dalam contoh sebelumnya) melibatkan rasio gaya seperti yang dicatat dalam Tabel 7.1. Kesetaraan dari pi term ini mengharuskan rasio gaya yang serupa di model dan prototipe menjadi sama. Dengan demikian, untuk aliran di mana nomor Reynolds sama, rasio gaya viskos dalam model dan prototipe sama dengan rasio gaya inersia. Ini lebih lanjut diilustrasikan oleh foto-foto di margin. Foto bagian atas adalah aliran melewati sebuah silinder dengan diameter, D, dan kecepatan, Vo, sementara kecepatan digandakan dan diameter dihaluskan pada foto bagian bawah (gambar ditunjukkan dengan pembesaran 2x). Karena nomor Reynolds cocok, aliran terlihat dan berperilaku sama. Jika pi term lainnya terlibat, seperti nomor Froude atau nomor Weber, kesimpulan serupa dapat ditarik; yaitu, kesetaraan dari pi term ini mengharuskan rasio gaya yang serupa di model dan prototipe menjadi sama.
Dengan demikian, ketika jenis pi term ini sama di model dan prototipe, kita memiliki kesamaan dinamis antara model dan prototipe. Ini mengikuti bahwa dengan adanya kesamaan geometris dan dinamis, pola garis arus akan sama dan rasio kecepatan yang sesuai (Vm/V2) dan rasio percepatan (am/a2) konstan di seluruh lapangan aliran. Dengan demikian, kesamaan kinematik ada antara model dan prototipe. Untuk memiliki kesamaan lengkap antara model dan prototipe, kita harus mempertahankan kesamaan geometris, kinematik, dan dinamis antara kedua sistem tersebut. Hal ini akan terjadi secara otomatis jika semua variabel penting disertakan dalam analisis dimensional, dan jika semua persyaratan kesamaan berdasarkan pi term yang dihasilkan terpenuhi.


