THE UPWIND SCHEME
Mempertimbangkan persamaan yang di-diskritisasi melalui skema upwind, tujuannya adalah untuk memulihkan persamaan integral sambil memperhitungkan kesalahan pemangkasan. Untuk melakukannya, ϕC dan ϕW ditulis sebagai fungsi dari ϕe dan ϕw, masing-masing, untuk kasus ketika aliran diasumsikan bergerak ke arah x positif. Dalam hal ini, skema upwind menghasilkan
Dengan demikian, persamaan difusi konveksi satu dimensi yang didiskritisasi menggunakan skema upwind disederhanakan menjadi

Ekspansi deret Taylor satu dimensi dari ϕC dengan memperhatikan nilai pada tepi sel e diberikan oleh:

dan untuk grid seragam sebagai:
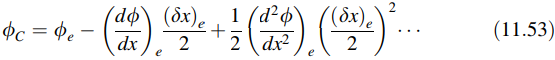
Ekspresi serupa dapat diperoleh untuk ϕW dan diberikan oleh:

Memotong suku orde kedua dan yang lebih tinggi serta mensubstitusi ke dalam suku adveksi, sisi kiri persamaan terdiskritisasi menjadi:

yang dapat diubah menjadi:

Sekarang jelas bahwa persamaan yang diselesaikan memiliki komponen tambahan difusi, yang disebut sebagai kesalahan pemotongan. Nilai difusi numerik adalah sama dengan
Kesalahan pemotongan ini, juga dikenal sebagai difusi sepanjang aliran, mengurangi akurasi solusi dengan mengubah magnitudo koefisien difusi dan akibatnya persamaan yang akan diselesaikan. Dengan demikian, persamaan adveksi dan difusi memiliki nilai modifikasi efektif dari efek difusi. Di sisi lain, difusi numerik tambahan ini diinginkan karena membuat solusi tetap stabil dengan tetap terbatas dan secara fisik benar. Jelas bahwa untuk mengurangi difusi numerik sepanjang aliran diperlukan pendekatan orde yang lebih tinggi dari suku adveksi. Namun, seperti yang akan dijelaskan dalam bagian selanjutnya, ini harus dilakukan sedemikian rupa sehingga solusi tetap terbatas.
