Time Derivatives

Konservasi massa dalam persamaan (2.8) termasuk turunan parsial terhadap waktu 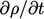yang berhubungan dengan suatu wilayah tetap dalam ruang. 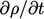adalah perubahan laju lokal dari (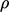) yang berhubungan dengan perubahan (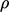) dalam fluida yang diukur oleh pengamat di lokasi tetap. Ini bukanlah laju perubahan waktu yang dialami oleh massa partikel fluida saat mereka bergerak melalui ruang. Dengan cara yang sama, 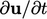bukanlah percepatan yang dialami oleh fluida.

Percepatan berkaitan dengan turunan material atau turunan substantif yang menggambarkan laju perubahan waktu dari suatu massa bahan yang bergerak tetap. Ini dilambangkan dengan (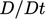 ) dan berkaitan dengan laju perubahan lokal, menggunakan (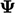) sebagai contoh tensor dari peringkat apa pun, dengan;

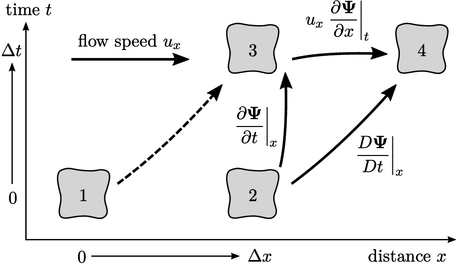
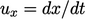Hubungan ini berasal dari aturan rantai diferensial. Dalam satu dimensi, hubungan ini diilustrasikan oleh dua partikel fluida yang menduduki posisi 1 dan 2 pada waktu awal tertentu, kemudian posisi 3 dan 4 pada waktu lebih lanjut ( $\text{[math]}$ ). Partikel bergerak dalam arah-x dengan kecepatan $\text{[math]}$ sehingga partikel di 1 kemudian menduduki posisi 3 dan partikel di 2 menduduki posisi 4.
Turunan waktu material dari ( 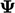$\text{[math]}$ ), mengikuti massa dari 2 -> 4, adalah jumlah dari perubahan lokal dari ( 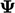$\text{[math]}$ ) di posisi tetap x (2 -> 3); dan perubahan akibat gradien ( 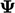$\text{[math]}$ ) antara posisi 3 dan 4, pada waktu tetap (t). Hal ini setara dengan

Hubungan turunan material dalam persamaan (2.14) adalah versi 3D dari persamaan (2.15)

Gradient

Suku terakhir dalam persamaan (2.14) memperkenalkan gradien yang dilambangkan dengan ( 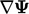$\text{[math]}$ ), Jika ( 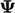$\text{[math]}$ ) adalah skalar, gradien menghasilkan suatu vektor yang magnitudonya dan arahnya adalah arah gradien tercuram.

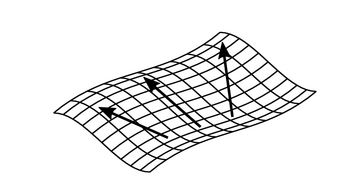
Gambar di samping menggambarkan gradien menggunakan suatu permukaan yang mewakili distibutif medan skalar dalam 2 arah. Gradien di 3 lokasi berada dalam arah kenaikan tercuram.
Ketika ( $\text{[math]}$ ) adalah vektor, gradien menghasilkan sebuah tensor, yang mewakili arah dan besarnya kenaikan tercuram untuk masing – masing dari 3 komponen dari vektor tersebut.