TU - infistream

TURBULENT CAMPURAN

Aliran turbulen ditandai oleh pencampuran yang signifikan dari pusaran fluida seperti yang ditunjukkan oleh eksperimen Reynolds di Bagian 6.1. Simulasi CFD umumnya perlu menyesuaikan pencampuran turbulen karena hal ini memengaruhi difusi massa, momentum, dan energi. Sementara pencampuran fluida melalui difusi massa itu sendiri bisa penting, efek pada difusi momentum seringkali kritis karena hal ini memengaruhi perhitungan gaya viskos dan, dengan demikian, aliran itu sendiri.

Eddy Viscosity (Viskositas Putaran)

Boussinesq adalah orang pertama yang merancang sebuah model untuk turbulensi. Dia mengakui kesamaan antara gerakan acak dari kedua pusaran dalam fluida turbulen dan partikel pada skala molekuler.

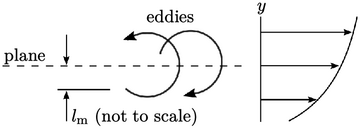
$PICT\relax \special {t4ht=$

Dengan analogi terhadap teori kinetik dalam Bagian 6.10, gaya geser akibat turbulensi disebabkan oleh momentum bersih, tegak lurus terhadap suatu bidang, akibat gerakan pusaran. Boussinesq mengaitkan gaya geser ini dengan gradien kecepatan melalui suatu viskositas pusaran (eddy viscosity) dalam persamaan .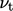

Dia menyajikan persamaan tekanan turbulen 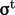dalam bentuk tensor, termasuk suatu tekanan. Teori kinetik menghubungkan tekanan dengan fluktuasi dalam persamaan kecepatan partikel 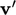dengan 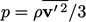;energi kinetik yang terkait dengan fluktuasi tersebut adalah persamaan 𝜌𝑣′ 2⁄2 . Dengan menerapkan argumen yang sama pada fluktuasi 𝑢′ kecepatan akibat turbulensi, menghasilkan suatu "tekanan" = 2⁄3 𝜌𝑘 turbulen 𝑘 = 𝑢′ 2⁄2 dalam persamaan, di mana persamaan adalah energi kinetik turbulen per unit massa.

Dengan analogi terhadap model fluida Newtonian Persamaan (2.41), model viskositas pusaran Boussinesq, yang menggabungkan persamaan 𝑘, adalah

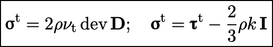|-------------------------------| ☐☐☐t =|2 tdev D; ☐☐☐t = ☐☐☐t 2- kI | --------------------------3------ \relax \special {t4ht=

(6.20)

di mana 𝜏t adalah komponen viskos dari tekanan Reynolds dan 𝐃 adalah tensor laju deformasi yang didefinisikan dalam Persamaan (2.33). Tidak terhindarkan bahwa Persamaan (6.20) dan Persamaan (2.41) mirip satu sama lain.

Model dari Persamaan (6.20) membutuhkan beberapa cara untuk menghitung 𝑣t. Teori kinetik memberikan prediksi kuantitatif dari 𝑣 dalam Persamaan (6.19) yang menyebabkan Boussinesq menghipotesiskan bahwa 𝑣t ∝ 𝑢 𝑙, di mana 𝑢 dan 𝑙 adalah kecepatan dan panjang yang representatif, masing-masing, dengan kecepatan 𝑢 berhubungan dengan 𝑢' karena turbulensi.

Viskositas turbulen juga dapat diungkapkan sebagai 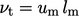dengan menyerap konstanta proporsionalitas dalam suatu kecepatan karakteristik um dan suatu panjang pencampuran 𝑙m, dibahas dalam Bagian 6.12.

Viskositas pusaran (eddy viscosity) dan panjang pencampuran (mixing length) adalah konsep-konsep yang berguna dalam pemodelan turbulensi. Namun, perlu diakui bahwa terdapat batasan dalam analogi dengan teori kinetik, misalnya:

• Momentum dipertukarkan antara partikel submikroskopis melalui tumbukan diskrit yang terputus-putus, dibandingkan dengan interaksi kontinu antara pusaran;

• Besarnya gerakan acak partikel umumnya sama dalam semua arah, sementara tingkat fluktuasi turbulen kadang-kadang dapat bervariasi secara signifikan dengan arah tertentu.