Turbin Impuls
Meskipun ada berbagai jenis desain turbin impuls, mungkin yang paling mudah dipahami adalah roda Pelton. Lester Pelton (1829–1908), seorang insinyur pertambangan Amerika, selama

era pertambangan emas California, bertanggung jawab atas banyak fitur yang masih digunakan dari jenis turbin ini. Turbin ini paling efisien saat dioperasikan dengan kepala yang besar (misalnya, sumber air dari danau yang terletak jauh di atas nozzle turbin), yang diubah menjadi kecepatan yang relatif besar di exit nozzle. Di antara banyak pertimbangan desain untuk turbin seperti ini adalah kerugian kepala yang terjadi dalam pipa (penstock) yang mengangkut air ke turbin, desain nozzle, dan desain bucket pada rotor.

Seperti yang ditunjukkan dalam Gambar 12.24, jet air berkecepatan tinggi menabrak bucket roda Pelton dan dibelokkan. Air masuk dan keluar dari volume kontrol yang mengelilingi roda sebagai jet bebas (pada tekanan atmosfer). Selain itu, seseorang yang naik di atas bucket akan melihat bahwa kecepatan air tidak berubah saat meluncur di atas bucket (dengan asumsi efek viscous dapat diabaikan). Artinya, magnitudo kecepatan relatif tidak berubah, tetapi arahnya berubah. Perubahan arah kecepatan jet fluida menyebabkan torsi pada rotor, yang menghasilkan daya output dari turbin.
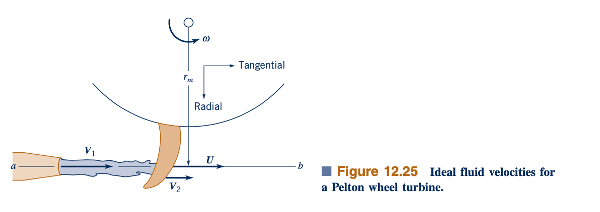
Merancang bentuk bucket yang optimum dan kompleks untuk memperoleh daya output maksimum adalah masalah yang sangat sulit. Idealnya, fluida masuk dan keluar dari volume kontrol yang ditunjukkan di Gambar 12.25 tanpa komponen kecepatan radial. (Dalam praktiknya, seringkali ada komponen radial yang kecil namun dapat diabaikan.) Selain itu, idealnya bucket akan memutar vektor kecepatan relatif melalui putaran 180°, tetapi kendala fisik menentukan bahwa b, sudut ujung keluar dari bilah, lebih kecil dari 180°. Oleh karena itu, fluida keluar dengan komponen kecepatan aksial seperti yang ditunjukkan dalam Gambar 12.26.
Segitiga kecepatan masuk dan keluar pada jari-jari rata-rata aritmetika, rm, diasumsikan seperti yang ditunjukkan dalam Gambar 12.27. Untuk menghitung torsi dan daya, kita harus mengetahui komponen tegak lurus dari kecepatan absolut di inlet dan outlet. (Ingat dari diskusi di Bagian 12.3 bahwa komponen radial maupun aksial dari kecepatan tidak masuk ke dalam persamaan torsi atau daya.) Dari Gambar 12.27, kita melihat bahwa
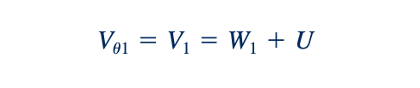

Dan
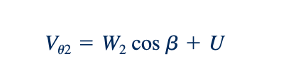
Dengan asumsi bahwa W=W' (artinya, kecepatan relatif fluida tidak berubah saat dibelokkan oleh bucket), kita dapat menggabungkan Persamaan 12.48 dan 12.49 untuk mendapatkan
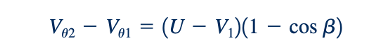
Perubahan dalam komponen tangensial kecepatan yang digabungkan dengan persamaan torsi dan daya yang dikembangkan dalam Bagian 12.3 (yaitu, Persamaan 12.2 dan 12.42) memberikan
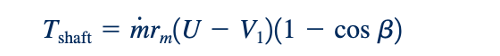
di mana m=pQ adalah laju aliran massa melalui turbin. Karena U=wR m , maka dapat disimpulkan bahwa

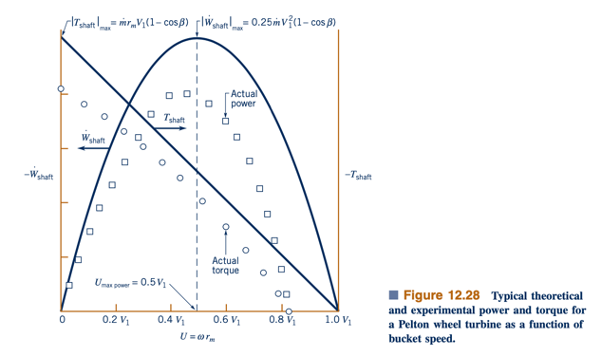
Hasil ini digambarkan dalam Gambar 12.28 bersama dengan hasil eksperimental khas. Perhatikan bahwa V > U (yaitu, jet memukul bucket), dan W < 0.
Beberapa poin menarik dapat dicatat dari hasil di atas. Pertama, daya adalah fungsi dari 𝛽. Namun, nilai tipikal 𝛽=165° (daripada optimum 180°) menghasilkan penurunan daya yang relatif kecil (kurang dari 2%) karena cos(165°)=1.966, dibandingkan dengan cos(180°)=2. Kedua, meskipun torsi maksimum terjadi ketika roda berhenti (U=0), tidak ada daya dalam kondisi ini — untuk mengekstrak daya, kita memerlukan gaya dan gerak. Di sisi lain, daya keluaran adalah maksimum saat
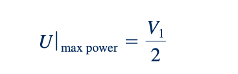
Ini dapat ditunjukkan dengan menggunakan Persamaan 12.51 dan menyelesaikan untuk U yang memberikan dW shaft/ dU=0. Kecepatan bucket setengah dari kecepatan fluida yang keluar dari nozzle memberikan daya maksimum. Ketiga, kecepatan maksimum terjadi ketika T shaft =0 (yaitu, beban sepenuhnya dihapus dari turbin, seperti yang akan terjadi jika poros yang menghubungkan turbin dengan generator putus dan torsi gesekan diabaikan). Untuk kasus ini U=wR=V1, turbin berputar bebas, dan air hanya melewati rotor tanpa memberikan gaya pada bucket.
Meskipun aliran sebenarnya melalui roda Pelton jauh lebih kompleks daripada yang diasumsikan dalam analisis sederhana di atas, hasil dan tren yang masuk akal diperoleh dengan penerapan sederhana prinsip momen-momentum.

Pada bab-bab sebelumnya, kita utamanya memperlakukan turbin (dan pompa) sebagai "kotak hitam" dalam aliran yang menghilangkan (atau menambahkan) energi pada fluida. Kita memperlakukan perangkat ini sebagai objek yang menghapus suatu kepala kerja poros tertentu dari atau menambahkan kepala kerja poros tertentu pada fluida. Hubungan antara kepala kerja poros dan daya keluaran seperti yang dijelaskan oleh pertimbangan momen-momentum diilustrasikan dalam Contoh 12.7.


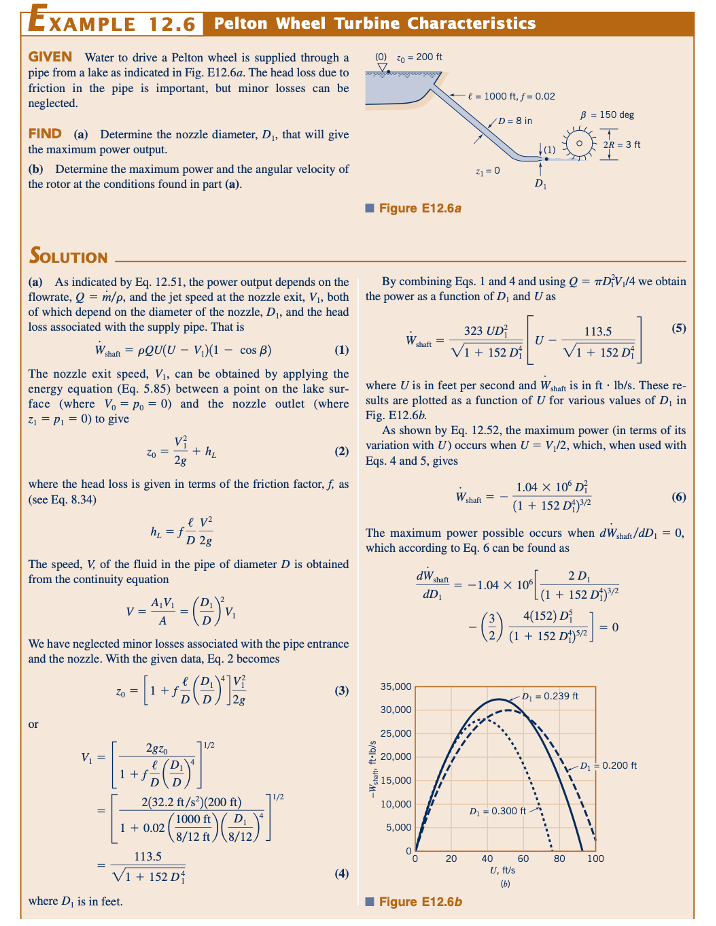
Jenis kedua turbin impuls yang banyak digunakan (biasanya dengan udara sebagai fluida kerja) ditunjukkan dalam Gambar 12.29. Serangkaian jet fluida memukul sudu-sudu berputar yang, seperti halnya dengan roda Pelton, mengubah arah dan besarnya kecepatan absolut. Seperti halnya dengan roda Pelton, tekanan masuk dan keluar (yaitu, di kedua sisi rotor) sama, dan besarnya kecepatan relatif tidak berubah saat fluida meluncur melintasi sudu-sudu (jika efek gesekan diabaikan).
Segitiga kecepatan masuk dan keluar yang khas (kecepatan absolut, relatif, dan sudu) ditunjukkan dalam Gambar 12.30. Seperti yang dibahas di Bagian 12.2, agar kecepatan absolut fluida berubah
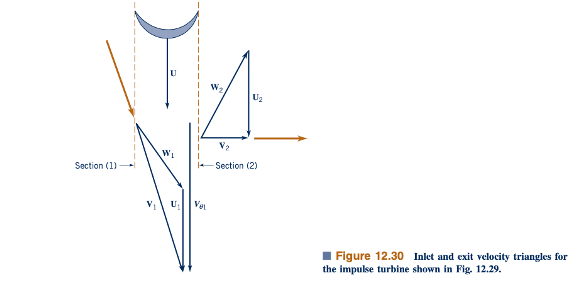
sebagaimana ditunjukkan selama perjalanannya melintasi sudu, sudu harus mendorong fluida ke arah berlawanan dari gerakan sudu. Oleh karena itu, fluida mendorong pada sudu searah dengan gerakan sudu — fluida melakukan kerja pada sudu (turbin).