TURBULENT KINETIC ENERGY
Persamaan tekanan turbulen πt dalam kekekalan momentum yang dirata-ratakan ensemble Persamaan (6.15) dapat diuraikan menjadi komponen viskos dan tekanan. Istilah tekanan turbulen, (2β3)ππ, sering kali dimasukkan dalam tekanan π, untuk memberikan.
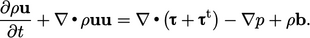 | (6.25) |
Gaya-gaya viskos dapat digabungkan dengan asumsi π dimodelkan sebagai fluida Newtonian Persamaan (2.41) dan πt oleh model viskositas pusaran Persamaan (6.20) untuk memberikan.
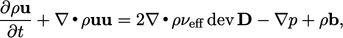 | (6.26) |
di mana viskositas kinematik efektif
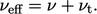 | (6.27) |
Viskositas kinematik efektif mewakili difusi momentum dari perpaduan gerakan molekuler dan turbulen. Sifat-sifat yang disebabkan oleh gerakan molekuler sering dijelaskan sebagai laminar, misalnya viskositas laminar π£.
Mengambil rata-rata persamaan momentum dan memperkenalkan model viskositas pusaran menciptakan satu variabel tambahan π£t. Model tambahan diperlukan untuk π£t untuk menyelesaikan sistem persamaan.
Dengan mempertimbangkan π£t = π’mπm dari Bagian 6.11, model untuk π£t biasanya didekomposisi menjadi komponen yang mewakili skala kecepatan dan panjang, π’m dan πm masing-masing.
Skala dari π’m sesuai dengan fluktuasi turbulen π’β², jadi wajar untuk mengasumsikan π’m πΌπ1β2 . Karena medan π mewakili komponen π’m dari π£t , ini umumnya diadopsi dalam model turbulensi berdasarkan π£t. Selain itu, hal ini dapat dengan baik direpresentasikan oleh persamaan konservasi yang sesuai.
Transport Turbulence Kinetic Energy
Persamaan konservasi energi kinetik turbulen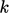Β Β 
Β dapat ditulis sebagai berikut :Β
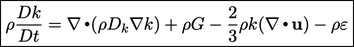 | (6.28) |
di mana persamaan pembangkitan turbulensi πΊ adalah
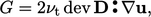 | (6.29) |
dan π·k ;adalah difusivitas efektif untuk π. Persamaan ini diperoleh dengan cara yang serupa dengan Persamaan (2.56) untuk konservasi energi internal spesifik π, dengan melakukan rata-rata (ensemble) terhadap kontribusi energi terpisah dari π’ dan π’β². Sementara melibatkan energi kinetik dari gerakan molekuler,π merupakan kesejajaran untuk gerakan pusaran.
Pada Persamaan (2.56), energi dari gerakan massa bergerak diubah ke skala submikroskopis sebagai panas oleh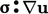 
. Pada Persamaan (6.28), energi tersebut diubah menjadi energi turbulen oleh 
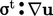menggunakan persamaan Boussinesq dari πt Persamaan (6.20). Komponen geser πt memberikan komponen yang tidak dapat dipulihkan 
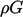pada Persamaan (6.28) dan istilah kedua ( π) menghasilkan 
..
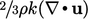Sementara 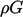mentransfer energi kinetik dari aliran massa ke π, istilah terakhir mentransfer ππ ke π sebagai panas π yang terdispersi. Di sini, π adalah laju dissipasi turbulen per unit massa dari dalam Bagian 6.6 yang, dari deduksi rata-rata ensemble pada Persamaan (6.28), adalah
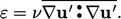 | (6.30) |
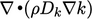di mana 
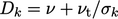. Ini mewakili difusi oleh gerakan dan interaksi molekuler dan
turbulen, termasuk koefisien yang dapat disesuaikan ππ yang biasanya diatur menjadi 1.