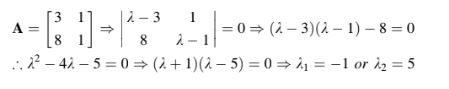2.3.4 Vektor Eigen dan Nilai Eigen
Vektor Eigen dan nilai Eigen. Pertimbangkan matriks persegi A dan vektor v. Vektor v adalah vektor eigen dari A jika hasil kali Av menghasilkan vektor yang memiliki arah yang sama dengan v [14–19]. Oleh karena itu, vektor eigen dari suatu matriks adalah vektor bukan nol yang tidak berputar ketika A diterapkan padanya. Seperti yang ditunjukkan pada Gambar 2.11, satu-satunya efek mungkin adalah mengubah panjangnya dan/atau membalik arahnya. Dengan demikian, ada skalar k sehingga Nilai k adalah eigenvalue dari A. Jelas bahwa untuk setiap konstanta a, vektor av juga merupakan vektor eigen dari A karena
Dengan demikian, vektor eigen yang telah di-skalar juga merupakan vektor eigen.
Jika A simetris berorde N, maka dapat ditunjukkan bahwa A memiliki set vektor eigen yang linearly independent, dilambangkan sebagaiSeperti yang dibuktikan di atas, set ini tidak unik. Namun, set yang sesuai dengan eigenvalues mereka, dilambangkan sebagai
yang mungkin atau mungkin tidak sama satu sama lain, adalah unik. Eigenvalues dari matriks identitas semuanya adalah satu, dan setiap vektor bukan nol adalah vektor eigen dari I.
Secara umum, eigenvalues dari matriks persegi A berorde N diperoleh dari menyelesaikan persamaan berikut:
Karena, menurut definisi, vektor eigen adalah vektor bukan nol, maka.
Bentuk yang diperluas dari Persamaan (2.48) diberikan oleh,

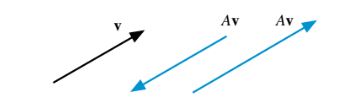
Gambar 2.11 Efek perkalian matriks A oleh salah satu vektor eigen v-nya,
Sebagai contoh, eigenvalue dari matriks persegi berorde 2 berikut ditemukan sebagai: