VISCOSITY ALAMI
Viscosity alami. Sebelum membahas turbulensi lebih lanjut, penting untuk memeriksa asal-usul viskositas. Viskositas diperkenalkan dalam Bagian 2.12 buku ini sebagai bagian dari model konstitutif Newtonian. Model ini awalnya bersifat fenomenologis, tetapi kemudian diperoleh secara langsung dari teori kinetik yang menggambarkan gas sebagai sejumlah partikel submikroskopis, misalnya atom atau molekul, dalam gerak acak.
Pandangan kinetik tentang viskositas membayangkan fluida dalam dua dimensi, 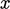 dan
dan 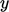 yang dikenai gaya geser dalam arah
yang dikenai gaya geser dalam arah 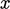 . Meskipun aliran rata-rata berada dalam arah ,partikel bergerak dalam arah
. Meskipun aliran rata-rata berada dalam arah ,partikel bergerak dalam arah 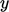 karena fluktuasi acak dengan kecepatan rata-rata
karena fluktuasi acak dengan kecepatan rata-rata 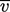 .
.
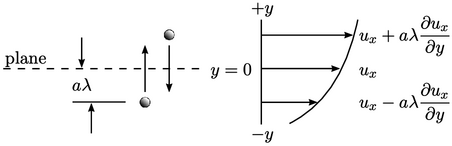
Misalkan sebuah pesawat berada pada persamaan 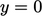 . Suatu partikel akan melewati suatu bidang jika jalurnya ke arah tersebut tidak terganggu oleh tumbukan yang menyebabkan partikel tersebut menjauh dari bidang tersebut. Partikel yang melewati bidang datang dari jarak rata-rata
. Suatu partikel akan melewati suatu bidang jika jalurnya ke arah tersebut tidak terganggu oleh tumbukan yang menyebabkan partikel tersebut menjauh dari bidang tersebut. Partikel yang melewati bidang datang dari jarak rata-rata 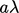 , di mana
, di mana  adalah beberapa faktor dari jarak rata-rata yang ditempuh oleh partikel yang bergerak antara tumbukan yang berurutan, rata-rata jalur bebas
adalah beberapa faktor dari jarak rata-rata yang ditempuh oleh partikel yang bergerak antara tumbukan yang berurutan, rata-rata jalur bebas 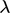 .
.
Dari teori kinetik, laju aliran massa partikel yang melewati permukaan dengan satuan luas 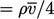 . Kecepatan rata-rata partikel yang melintasi bidang dari arah yang sama adalah
. Kecepatan rata-rata partikel yang melintasi bidang dari arah yang sama adalah 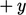 ; demikian pula dari arah
; demikian pula dari arah 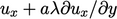 , sebanding dari arah
, sebanding dari arah 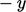 yaitu
yaitu 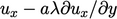 .
.
Momentum 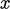 bersih partikel, positif di sisi
bersih partikel, positif di sisi 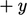 dari bidang tersebut
dari bidang tersebut
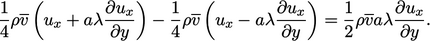 (6.16)
(6.16)Momem neto setara dengan tegangan geser 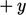 di sisi bidang,
di sisi bidang, 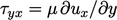 ,sebagaimana dijelaskan pada Bagian 2.6. Dibandingkan dengan Persamaan (6.16), persamaan viskositas dinamis
,sebagaimana dijelaskan pada Bagian 2.6. Dibandingkan dengan Persamaan (6.16), persamaan viskositas dinamis 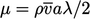 dalam hal sifat- sifat molekuler. Viskositas kinematik adalah
dalam hal sifat- sifat molekuler. Viskositas kinematik adalah
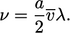 | (6.17) |
Analisis asli Maxwell menggunakan persamaan 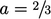 dalam Persamaan (6.17). Kemudian diakui bahwa jarak rata-rata yang dijelaskan oleh persamaan lebih besar karena adanya kelanjutan kecepatan, yaitu sebuah partikel kadang-kadang akan mempertahankan jalur menuju bidang setelah suatu tumbukan.
dalam Persamaan (6.17). Kemudian diakui bahwa jarak rata-rata yang dijelaskan oleh persamaan lebih besar karena adanya kelanjutan kecepatan, yaitu sebuah partikel kadang-kadang akan mempertahankan jalur menuju bidang setelah suatu tumbukan.
Analisis yang lebih mendalam dimulai dengan persamaan Boltzmann dan menerapkan ekspansi Chapman–Enskog hingga orde pertama dalam bilangan Knudsen.
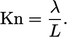 | (6.18) |
Analisis ini menurunkan hukum-hukum kekekalan dengan model konstitutif Newtonian dan Fourier, yaitu Persamaan (2.19), Persamaan (2.51), Persamaan (2.41), dan Persamaan (2.54). Dengan memperlakukan partikel sebagai bola-bola yang kaku dan tumbukan sebagai elastis, menghasilkan nilai persamaan 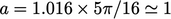 , ,meninggalkan ekspresi sederhana untuk viskositas yang adalah
, ,meninggalkan ekspresi sederhana untuk viskositas yang adalah
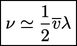 | (6.19) |
