VORTICITY TRANSPORT
Vorticity Transport. Untuk fluida yang tidak dapat dipampatkan (dengan asumsi sederhana lainnya), vortisitas mematuhi persamaan transportasi, Persamaan (6.2). Ini adalah persamaan adveksi-difusi khas, serupa dengan Persamaan (2.65) untuk panas, yang diungkapkan dalam hal turunan waktu lokal dan adveksi dalam bentuk konservatif oleh
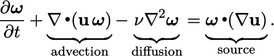 | (6.1) |
Terutama, Persamaan (6.1) tidak termasuk suku dalam p. Ini berbeda dengan hukum kekekalan momentum (linear) yang dapat mendistribusikan gangguan dalam u secara instan di seluruh domain melalui persamaan 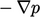 seperti yang dibahas di Bagian 2.22.
seperti yang dibahas di Bagian 2.22.
Sebaliknya, seperti panas, vortisitas berkembang secara lokal saja, dengan rentang pengaruh terbatas oleh adveksi dan transport difusi, seperti yang dibahas di halaman 126.
Adveksi vortisitas jelas diilustrasikan oleh cincin asap yang ditunjukkan di Bagian 2.11.
Difusi terjadi melalui torsi viscous yang mentransfer momentum sudut antara elemen fluida.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
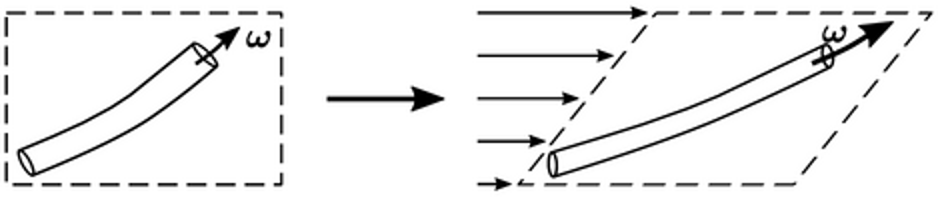
Sumber vortisitas, 𝜔. (∇𝜐) Persamaan , disebabkan oleh pusaran yang mengubah bentuknya di bawah pengaruh gradien kecepatan ∇𝜐. Jika sebuah pusaran diregangkan, misalnya di bawah gaya geser seperti yang ditunjukkan di atas, jari-jarinya akan menyusut, sehingga kecepatan sudut, dan dengan 𝜔 demikian vortisitas, meningkat. Demikian pula, 𝜔 vortisitas akan berkurang jika pusaran tersebut dipersempit.
Persamaan Transport Voritcity
Untuk aliran tak terkompresibel dengan nilai tetap untuk kecepatan suara 𝜈 (dan gaya tubuh nol, atau tetap), vortisitas mematuhi persamaan transportasi berikut:
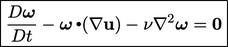 | (6.2) |
Persetujuan dari hukum kekekalan momentum untuk fluida homogen, tak terkompresibel, Newtonian dengan kecepatan suara 𝜈= konstan dan mengabaikan gaya-gaya tubuh, Persamaan (2.49), menghasilkan ∇. (𝑢 𝑢)= 𝜐 . ∇ 𝑢 Persamaan (2.46) yang menyebabkan
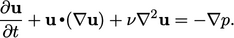 | (6.3) |
Persamaan vortisitas berasal dari rotasional (∇× ) dari Persamaan (6.3) yang digabungkan dengan definisi vortisitas Persamaan (2.37). Istilah pertama adalah 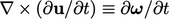 ..
..
Menggantikan 𝛼 dan b dengan 𝑢 dalam Persamaan (2.72d) dan menerapkan Persamaan (2.37) memberikan
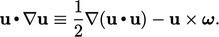 | (6.4) |
Curl dari istilah kedua dalam Persamaan (6.3) dinyatakan oleh curl dari Persamaan (6.4) dengan Persamaan (2.75a), Persamaan (2.73a), Persamaan (2.75e), dan Persamaan (2.46), menghasilkan
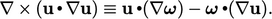 | (6.5) |

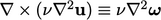 dihitung dengan menggunakan Persamaan (2.74f). Curl dari istilah keempat
dihitung dengan menggunakan Persamaan (2.74f). Curl dari istilah keempat 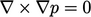
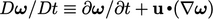 Eq. (6.5), menghasilkan Persamaan (6.2).
Eq. (6.5), menghasilkan Persamaan (6.2).