Internal Energi

Internal energi

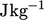Konservasi energi, pada Persamaan (2.51), memperkenalkan energi dalam kuantitas tertentu $persamaan$ , diukur dalam $persamaan$ satuan SI. Ini mewakili energi molekul total yang terdiri dari; energi kinetik yang berhubungan dengan suhu; energi potensial akibat gaya partikel, baik di dalam partikel sebagai ikatan kimia, maupun antar partikel, seperti gaya van der Waals.

Energi pada skala yang berbeda dapat diringkas sebagai:

massal — kinetik 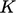$persamaan$ akibat gerak massal, potensial akibat gaya 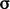$persam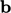aan$ dan $persamaan$ ;
molekuler — kinetik yang dicirikan oleh 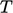$persamaan$ , potensial akibat ikatan.

Untuk memahami bagaimana energi ditransfer antara skala-skala ini, kita dapat memperoleh persamaan energi dalam dari Persamaan. (2.51), dengan menghilangkan suku-suku energi mekanik yang dibentuk dengan mengambil hasil kali dalam Persamaan. (2.19) dengan 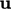$persamaan$ .

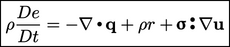|--------------------------| |De- | Dt| = r q + r + ☐☐☐ ru | ---------------------------- \relax \special {t4ht=

(2.56)

Identitas 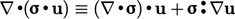$persamaan$ adalah elemen kunci dari analisis. Istilah 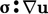$persamaan$ dalam Persamaan. (2.56) harus mewakili kontribusi tenaga mekanik terhadap energi internal, yaitu berpindah dari skala besar ke skala molekuler. Sebaliknya, 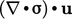$persamaan$ istilah tersebut harus menyumbang energi mekanik.

Mengganti 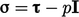$persamaan$ dari Persamaan. (2.41), Persamaan. (2.56) menjadi

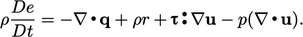De- = r q + r + ☐☐☐ ru p(r u): Dt \relax \special {t4ht=

(2.57)

Tandanya 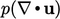$persamaan$ bergantung pada 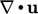$persamaan$ , yaitu apakah fluida mengembang atau menyusut. Karena tanda dapat berubah, maka tanda tersebut mewakili kontribusi energi internal yang dapat dipulihkan .

Jika kita mengganti model Newton dari Persamaan. (2.41)

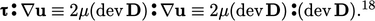☐☐☐ ru 2 (devD) ru 2 (dev D) (dev D):18 \relax \special {t4ht=

(2.58)

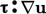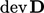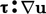Istilahnya $persamaan$ selalu positif karena semua komponennya $persamaan$ dikuadratkan. $persamaan$ Oleh karena itu, kontribusinya tidak dapat diperoleh kembali dan mewakili tenaga mekanik yang hilang sebagai panas. Pada sebagian besar analisis CFD, kontribusinya $persamaan$ kecil dan dapat diabaikan.

Hasil kali dalam ganda dari dua tensor

Hasil kali dalam ganda dari dua tensor, dilambangkan dengan “ $persamaan$ ”, diperkenalkan pada Persamaan. (2.56). Ini menghasilkan skalar yang dievaluasi sebagai jumlah dari 9 produk komponen tensor, misalnya:

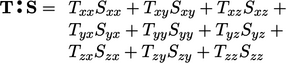T S = TxxSxx + TxySxy + TxzSxz + TyxSyx + TyySyy + TyzSyz + T S + T S + T S zx zx zy zy zz zz \relax \special {t4ht=

(2.59)

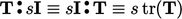Untuk skalar $persamaan$ , $persamaan$ .