Introducing the Finite Volume Method in OpenFOAM
Introducing the Finite volume method in openFOAM. Sebuah tinjauan tentang Metode Volume Hingga (FVM) dalam OpenFOAM disajikan dalam artikel ini. Deskripsi yang lebih detail tentang FVM dapat ditemukan di Ferziger dan Perić [1], Versteeg dan Malalasekra [13], Weller, Tabor, Jasak, dan Fureby [14], Jasak, Jemcov, dan Tuković [4], dan Moukalled, Mangani, Darwish, dkk. [6] untuk deskripsi yang lebih detail.
Langkah-langkah FVM terstruktur dalam OpenFOAM berkorelasi dengan beberapa langkah analisis CFD yang dijelaskan dalam bagian 1.2. Properti fisik yang menentukan aliran fluida, seperti tekanan, kecepatan, atau suhu/entalpi adalah variabel dependen dalam model matematika: deskripsi matematis formal dari aliran fluida. Model matematika yang menggambarkan aliran fluida didefinisikan sebagai sistem PDE.
Berbagai proses fisik kadang-kadang dijelaskan menggunakan deskripsi matematis yang serupa, seperti konduksi panas serta difusi konsentrasi gula dalam air dimodelkan sebagai proses difusif. Persamaan transportasi skalar umum, seperti yang dijelaskan dalam [1], mengandung istilah (operator diferensial) yang memodelkan berbagai proses fisik, misalnya: transportasi partikel dengan kecepatan fluida (istilah adveksi), sumber panas (istilah sumber), dan sebagainya. Karena mengandung istilah yang sering dijumpai, persamaan transportasi skalar umum digunakan untuk menggambarkan FVM, dengan cara mendiskritisasi
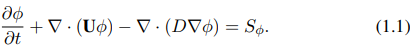
Di sini, φ adalah properti skalar yang diangkut, U adalah kecepatan yang ditentukan dan D adalah koefisien difusi. Namun istilah dalam persamaan (1.1) dari kiri ke kanan adalah: istilah temporal, istilah konvektif, istilah difusif, dan istilah sumber. Setiap istilah menggambarkan proses fisik yang mengubah properti φ dengan cara yang berbeda.
Bergantung pada sifat prosesnya, beberapa istilah mungkin diabaikan: misalnya untuk aliran fluida inviscid, istilah difusif (transportasi) momentum diabaikan dalam persamaan momentum. Selain itu, koefisien yang muncul dalam beberapa istilah mungkin nilai konstan, lapangan yang bervariasi spasial/temporal, atau tergantung pada properti fisik. Contoh koefisien yang tergantung adalah koefisien konduktivitas yang tergantung pada suhu untuk transfer panas konduktif: ∇·(k(T)∇T), yang membuat k menjadi medan yang bervariasi spasial/temporal yang akan tergantung pada solusi model: medan suhu.
Tujuan dari metode numerik apapun adalah untuk mendekati solusi dari model matematika. Pendekatan solusi dari proses fisik yang kompleks diperlukan karena solusi eksak dapat diperoleh untuk kasus yang sangat khusus yang sering kali kurang relevan untuk aplikasi teknis atau rekayasa.

Gambar 1.1: Domain aliran kontinu dan terdiskritisasi beserta variabel aliran kontinu dan diskrit yang sesuai.
Solusi aproksimatif (pendekatan) dari model matematika diperoleh dengan memecahkan pendekatan diskrit dari sistem persamaan governing. Proses aproksimasi Metode Volume Hingga (FVM) melibatkan substitusi sistem PDE dengan sistem persamaan aljabar linear yang sesuai, yang selanjutnya dapat diselesaikan menggunakan komputer. Implementasi sistem persamaan aljabar oleh Metode Volume Hingga (FVM) terstruktur terdiri dari dua langkah utama: diskritisasi domain dan diskritisasi persamaan.
