Jet Gratis
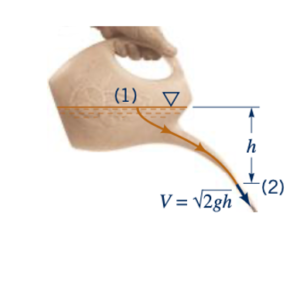
Salah satu persamaan tertua dalam mekanika fluida membahas aliran cairan dari sebuah wadah besar. Sebuah versi modern dari jenis aliran ini melibatkan aliran kopi dari sebuah dapur kopi seperti yang ditunjukkan oleh gambar di pinggiran. Prinsip dasar dari jenis aliran ini ditunjukkan dalam Gambar 3.11 di mana sebuah jet cairan berdiameter d mengalir dari nosel dengan kecepatan V. Aplikasi Persamaan 3.17 antara titik 112 dan 122 pada streamline yang ditunjukkan memberikan
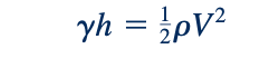
Kami telah menggunakan fakta bahwa z1= h, z2=0, reservoirnya besar (V1=0) dan terbuka ke atmosfer (p1=0 gage), dan fluida keluar sebagai "jet bebas" (p2= 0). Dengan demikian, kami mendapatkan
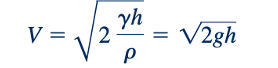
ini adalah versi modern dari hasil yang diperoleh pada tahun 1643 oleh Torricelli (16030-1647), seorang fisikawan Italia.
Fakta bahwa tekanan keluar sama dengan tekanan sekitar (p2 = 0) dapat dilihat dengan menerapkan F=ma, seperti yang diberikan oleh Persamaan 3.14, melintasi aliran garis-garis arus antara (2) dan (4). Jika garis arus di ujung nozzle adalah lurus (R = ∞), maka berlaku p2=p4 . Karena (4) berada pada permukaan dari jet, yang berkontak dengan atmosfer, kita memiliki p4= 0. Dengan demikian, p2=0 juga. Karena (2) adalah titik sembarang di bidang keluar dari nozzle, maka tekanannya adalah atmosfer di seluruh bidang ini. Secara fisik, karena tidak ada komponen gaya berat atau percepatan dalam arah normal 1horizontal2, tekanan konstan dalam arah itu.
Setelah keluar dari nozzle, aliran terus jatuh sebagai jet bebas dengan tekanan nol di seluruh (p5=0) dan seperti yang terlihat dengan menerapkan Persamaan 3.17 antara titik (1) dan (5), kecepatannya meningkat sesuai dengan
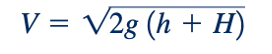
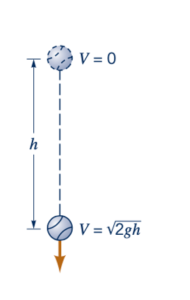
di mana, seperti yang ditunjukkan dalam Gambar 3.11, H adalah jarak yang telah ditempuh cairan di luar nozzle.
Persamaan 3.18 juga bisa diperoleh dengan menulis persamaan Bernoulli antara titik (3) dan (4). Seperti yang dipelajari dalam fisika atau dinamika dan diilustrasikan dalam gambar di samping z4=0, z3, V3=0 setiap benda yang dilepaskan dari keadaan diam dan jatuh melalui jarak h dalam hampa udara akan memperoleh kecepatan V=√2𝑔ℎ, sama seperti air yang keluar dari keran penyiram yang ditunjukkan dalam gambar di samping. Ini konsisten dengan fakta bahwa seluruh energi potensial partikel diubah menjadi energi kinetik, asalkan efek viskos (gesekan) diabaikan. Dalam hal kepala, kepala elevasi di titik (1) diubah menjadi kepala kecepatan di titik (2). Ingat bahwa untuk kasus yang ditunjukkan dalam Gambar 3.11 tekanannya sama (atmosfer) di titik (1) dan (2).
Untuk nozzle horizontal seperti pada Gambar 3.12a, kecepatan cairan di garis tengah, V2, akan sedikit lebih besar daripada di bagian atas, V1, dan sedikit lebih kecil daripada di bagian bawah, V3, karena perbedaan elevasi. Secara umum, d h seperti yang ditunjukkan dalam d< h Gambar 3.12b dan kita dapat dengan aman menggunakan kecepatan garis tengah sebagai "kecepatan rata-rata" yang wajar.
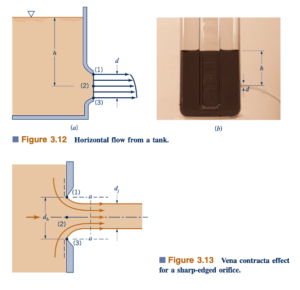
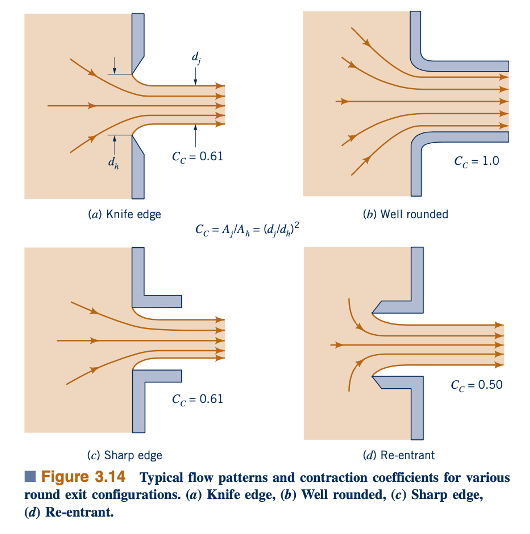
Jika keluaran bukanlah nozzle yang halus dan berkontur baik, melainkan sebuah pelat datar seperti yang ditunjukkan dalam Gambar 3.13, diameter jet, dj, akan lebih kecil daripada diameter lubang, ℎd . Fenomena ini, yang disebut efek vena contracta, adalah hasil dari ketidakmampuan fluida untuk membelokkan sudut tajam 90° seperti yang ditunjukkan oleh garis putus-putus dalam gambar.
Karena garis arus di bidang keluar melengkung (r<∞), tekanan di sepanjang garis arus tersebut tidak konstan. Diperlukan gradien tekanan tak terhingga di sepanjang garis arus untuk menyebabkan fluida berbelok pada sudut yang "tajam" (r=0). Tekanan tertinggi terjadi di sepanjang garis tengah pada titik (2) dan tekanan terendah p1= p3 =0, berada di tepi jet. Oleh karena itu, asumsi kecepatan seragam dengan garis arus lurus dan tekanan konstan tidak berlaku di bidang keluar. Namun, asumsi tersebut valid di bidang vena contracta, bagian a-a. Asumsi kecepatan seragam valid di bagian ini asalkan dj≈ℎ, seperti yang dibahas untuk aliran dari nozzle yang ditunjukkan dalam Gambar 3.12.
Efek vena contracta adalah fungsi dari geometri outlet. Beberapa konfigurasi khas ditunjukkan dalam Gambar 3.14 bersama dengan nilai-nilai tipikal dari koefisien kontraksi yang diperoleh secara eksperimental, Cc=Aj/Ah , di mana Aj dan ℎA adalah luas jet di vena contracta dan luas lubang, masing-masing.