kECEpatan masuk tidak seragam

Kecepatan masuk tidak seragam. Pada batas saluran masuk, kecepatan biasanya ditentukan oleh kondisi nilai tetap 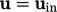$persamaan$ , seperti dibahas dalam Bagian. 4.3. Dalam banyak aplikasi CFD, aliran pada batas saluran masuk digambarkan dengan kecepatan tunggal yang diterapkan pada semua permukaan dengan asumsi 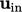$persamaan$ seragam melintasi batas tersebut.

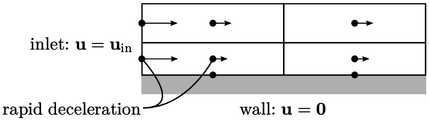
$GAMBAR\santai \khusus {t4ht=$

Hal ini menciptakan anomali dimana batas saluran masuk bertemu dengan dinding. Di sekitar dua batas tersebut, kecepatan aliran melambat dari 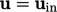$persamaan$ permukaan saluran masuk ke nilai pada sel yang berdekatan mendekati kondisi tanpa selip 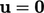$persamaan$ yang diterapkan pada dinding.

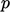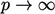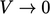Pasti ada “lonjakan” tekanan dan tegangan geser yang tinggi di dalam sel untuk memperlambat aliran dengan begitu cepat. Ketika panjang sel (dalam arah aliran) berkurang, perlambatan dan tekanan yang terkait $persamaan$ meningkat sedemikian rupa sehingga $persamaan$ membatasi volume sel $persamaan$ .

Solusinya cenderung menyatu lebih lambat seiring dengan lonjakan tekanan, dan bisa jadi tidak stabil. Selain itu, lonjakan tegangan geser dapat menghasilkan turbulensi tingkat tinggi yang dapat menyebabkan pemisahan aliran pada pertemuan saluran masuk dan dinding.

Kondisi seragam tidak mencerminkan perilaku aliran di hulu saluran masuk. Misalnya, dengan asumsi dinding memanjang ke arah hulu, lapisan batas akan terbentuk di saluran masuk; atau jika dinding dimulai dari saluran masuk, aliran akan terhenti di tepi depannya.

Ini adalah contoh yang baik dari aksioma bahwa metode numerik tidak merespon dengan baik terhadap pemodelan apa pun yang tidak bersifat fisik. Masalah ini dapat dihindari dengan menentukan ketidakseragaman 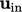$persamaan$ yang mewakili aliran hulu dengan lebih baik.

Beberapa bidang teknik menggunakan teori yang sudah ada untuk menggambarkan saluran masuk 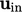$persamaan$ , misalnya teknik angin menggunakan profil berdasarkan 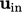$persamaan$ lapisan batas atmosfer di sepanjang permukaan bumi.

Secara umum, nonuniform 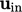$persamaan$ dapat ditentukan yang cenderung berada 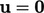$persamaan$ pada batas dinding. Profil dapat digambarkan dengan 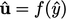$persamaan$ dimana: 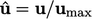$persamaan$ adalah kecepatan yang dinormalisasi dan 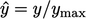$persamaan$ jarak yang dinormalisasi ke batas dinding terdekat; dan, $persam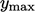aan$ dan $persamaan$ menunjukkan nilai maksimum $persamaan$ dan $persamaan$ .

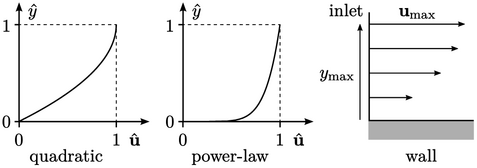
$GAMBAR\santai \khusus {t4ht=$

Adalah logis untuk menentukan 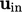$persamaan$ menggunakan profil yang telah ditetapkan untuk lapisan batas sebagai perkiraan yang masuk akal untuk kondisi hulu. Fungsi kuadrat 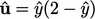$persamaan$ mewakili lapisan batas yang dikembangkan untuk aliran laminar, yang sesuai dengan profil analitis untuk aliran dalam pipa atau antara pelat datar paralel, yaitu hukum Poiseuille.

Sebagai alternatif, fungsi hukum pangkat 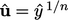$persamaan$ mewakili lapisan batas turbulen yang berkembang dengan cukup baik. Prandtl menggunakan — hukum pangkat sepertujuh 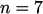$persamaan$ miliknya — untuk mereproduksi data aliran dalam pipa, tetapi eksponen apa pun yang sesuai $persamaan$ dapat digunakan dalam praktik.