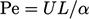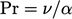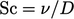Kesamaan Skala

Kesamaan skala adalah gagasan bahwa untuk dua sistem yang serupa secara geometri, aliran akan mengikuti jalur yang sama jika rasio besar gaya yang bekerja pada fluida adalah sama pada titik-titik aliran yang berbeda.

Aliran pada skala yang berbeda dapat dibandingkan dengan menggunakan variabel tak berdimensi. Persamaan momentum, pada Persamaan (2.67), dengan gaya adveksi, difusi dan gravitasi, dapat dinyatakan dalam bentuk non-dimensi dengan;

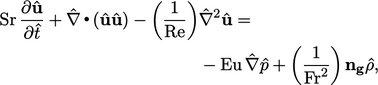Sr @^u-+ ^r (^u^u) 1-- ^r2u^= @^t Re ^ -1- Eu r^p + Fr2 ng ^; \relax \special {t4ht=

(2.68)

dengan bilangan tak berdimensi:

Nomor Strouhal 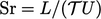$persamaan$ — inersia sementara/stabil;
bilangan Reynolds 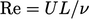$persamaan$ — gaya inersia/kental;
bilangan Euler 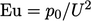$persamaan$ — gaya tekanan/inersia;
(Nomor palsu) 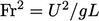$persamaan$ $persamaan$ — gaya inersia/gravitasi.

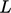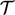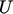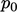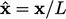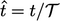Bilangan tak berdimensi ini mencakup karakteristik panjang $persamaan$ , waktu $persamaan$ , kecepatan $persamaan$ , dan tekanan $persamaan$ . Notasi $persamaan$ (topi) menunjukkan panjang tak berdimensi, waktu, dll. Misalnya, $persamaan$ , $persamaan$ dan operator tak berdimensi terkait 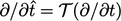$persamaan$ dan 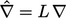$persamaan$ .

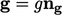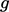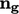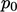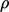Persamaan 2.68 mengasumsikan konstan $persamaan$ membagi percepatan gravitasi $persamaan$ ke dalam besaran $persamaan$ dengan arah satuannya $persamaan$ . Tekanan, termasuk $persamaan$ , dalam satuan kinematik (dibagi dengan $persamaan$ ).

Bilangan tak berdimensi memberikan perbandingan besaran gaya fluida yang berbeda. Misalnya, 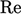$persamaan$ mewakili rasio gaya inersia terhadap gaya viskos dan memainkan peran penting dalam pemodelan turbulensi, yang diperkenalkan pada Bab 6.

Kesamaan skala juga berlaku untuk properti yang diangkut lainnya. Misalnya persamaan energi, pada Persamaan (2.65), mengabaikan sumber panas $persamaan$ dan dapat dinyatakan dalam bentuk non-dimensi sebagai berikut;

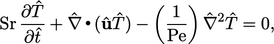@ ^T ^ ^ -1- ^2 ^ Sr @^t + r (^u T) Pe r T = 0; \relax \special {t4ht=

(2.69)

dengan mencakup bilangan tak berdimensi tambahan seperti berikut :

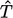Nomor peclet $persamaan$ — adveksi/difusi panas.

Sekali lagi pada Persamaan (2.69), $persamaan$ notasi (topi) diterapkan pada suhu $persamaan$ untuk menunjukkan suhu tak berdimensi, meskipun notasi tersebut tidak muncul dalam bilangan tak berdimensi.

Faktanya, dengan pengecualian momentum (yang menggunakan 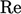$persamaan$ ), $persamaan$ secara lebih umum mewakili laju adveksi dan difusi, sebagai rasio untuk kuantitas apa pun yang diangkut (dalam hal ini, panas).

Angka selanjutnya tentukan rasio diﬀusivitas, misalnya :

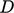Nomor Prandtl $persamaan$ — viskositas/difusivitas termal;
nomor Schmidt $persamaan$ — viskositas/difusi massa.

di mana $persamaan$ difusivitas massa (tidak dibahas dalam buku ini).

Bilangan tak berdimensi dapat dikalikan dan dibagi satu sama lain untuk membentuk bilangan tak berdimensi selanjutnya. Misalnya bilangan Péclet untuk perpindahan panas 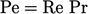$persamaan$ . seper