8.3 Kondisi Batas
Dikenal bahwa solusi analitis untuk setiap persamaan diferensial biasa atau parsial diperoleh hingga beberapa konstanta yang ditetapkan oleh kondisi batas yang berlaku untuk situasi yang sedang dipelajari. Oleh karena itu, penggunaan kondisi batas yang berbeda akan menghasilkan solusi yang berbeda meskipun persamaan umum tetap sama. Solusi numerik mengikuti kendala yang sama, memerlukan implementasi kondisi batas yang benar dan akurat karena setiap perubahan kecil dalam kondisi ini yang diperkenalkan oleh aproksimasi numerik dapat menyebabkan solusi yang salah dari masalah yang sedang dipertimbangkan. Kondisi batas akan dibahas sesuai dengan yang dianggap relevan untuk istilah-istilah yang didiskritisasi. Untuk masalah konduksi/difusi, ditemui jenis kondisi batas Dirichlet, Neumann, campuran, dan simetri, yang akan dijelaskan selanjutnya. Kondisi batas diterapkan pada elemen batas, yang memiliki satu atau lebih wajah di batas. Nilai-nilai diskrit φ disimpan baik di sentroid sel batas maupun di sentroid wajah batas. Misalkan C menunjukkan sentroid elemen batas yang ditunjukkan pada Gambar 8.3 dengan satu wajah batas dari sentroid b dan vektor permukaan Sb yang mengarah ke luar. Seperti sebelumnya, proses diskritisasi di atas sel C menghasilkan
Fluks pada wajah-wajah interior didiskritisasi seperti sebelumnya, sementara fluks batas didiskritisasi dengan tujuan membangun linearisasi terhadap φC, dengan demikian
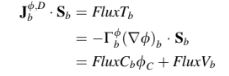
Spesifikasi kondisi batas melibatkan pengaturan nilai batas yang tidak diketahui atau sebagai alternatif, fluks batas
Menggunakan Persamaan (8.18), persamaan terdiskritisasi pada suatu elemen batas untuk berbagai jenis kondisi batas pada masalah difusi akan dihasilkan selanjutnya.
