konservasi energi

Konservasi Energi
- Hukum kekekalan energi menyatakan bahwa total energi dari suatu sistem terisolasi akan selalu konstan dari waktu ke waktu. Energi tidak diciptakan atau dimusnahkan, namun diubah dari satu bentuk menjadi bentuk lainnya. Jika kita mempertimbangkan energi mekanik dan termal, hal ini dapat diungkapkan oleh persamaan:
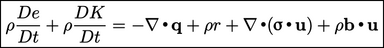 | (2.51) |
- Persamaan tersebut menggambarkan laju perubahan energi mekanik dan termal untuk suatu volum material dari partikel fluida dengan massa tetap. Energi termal dijelaskan oleh energi internal spesifik, e, dimana spesifik mengacu pada per unit massa. Energi mekanik direpresentasikan oleh energi kinetik spesifik
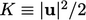 .
.
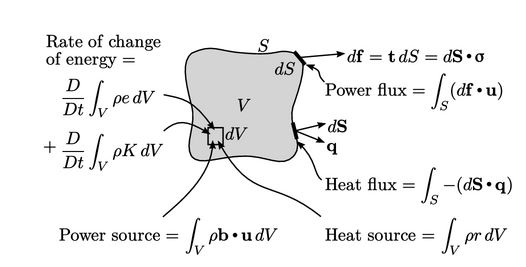
- Laju perubahan dari energi-energi gabungan ini disebabkan oleh masukan daya mekanik dan panas dari kedua fluks permukaan dan sumber internal.
- Daya mekanik dihitung sebagai hasil dari gaya dan kecepatan (u). Daya atas segmen permukaan dS adalah
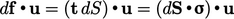 , yang mewakili perubahan energi regangan. Sumber daya internal adalah
, yang mewakili perubahan energi regangan. Sumber daya internal adalah 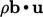 , yang mewakili perubahan energi potensial akibat gaya-gaya umum pada sebuah bentuk (body).
, yang mewakili perubahan energi potensial akibat gaya-gaya umum pada sebuah bentuk (body). - Panas disediakan oleh sumber internal dengan kekuatan r per unit massa dan fluks panas permukaan q per unit luas permukaan. Fluks panas permukaan yang terkait dengan panas input mengambil tanda negatif,
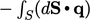 , karena q mengikuti konvensi menunjukkan kondisi keluar sistem.
, karena q mengikuti konvensi menunjukkan kondisi keluar sistem. - Persamaan 2.15 diperoleh dengan menyamakan integral dari laju perubahan energi terhadap daya mekanik dan panas input, serta mengambil
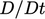 ke dalam integral volume karena pdV eqn konstan dari waktu, sebagai berikut :
ke dalam integral volume karena pdV eqn konstan dari waktu, sebagai berikut :
![Z De- + DK-- dV = V Dt Dt Z Z [ dS q + (dS ☐☐☐) u] + [ r + b u] dV: S V \relax \special {t4ht=](https://doc.cfd.direct/notes/cfd-general-principles/img/index663x.png) | (2.52) |
- Teorema Gauss mengonversi integral permukaan dari Pers. (2.52) menjadi integral volume berikut:
![Z [ r q + r (☐☐☐ u)] dV: V \relax \special {t4ht=](https://doc.cfd.direct/notes/cfd-general-principles/img/index664x.png) | (2.53) |
- Dengan mensubstitusikan Pers. (2.53) untuk integral permukaan ke dalam Pers. (2.52) dan menyamakan integrannya dengan 0, seperti yang dijelaskan sebelumnya dalam Bagian 2.7, menghasilkan Pers. (2.51)
