Konveksi Alami

Konveksi Alami.

Pada bagian 2.13, satu set persamaan — Persamaan (2.47) dan Persamaan (2.48) — diturunkan untuk aliran fluida yang tidak dapat dimampatkan. Ini adalah contoh kumpulan persamaan kekekalan massa dan momentum yang dapat diselesaikan dengan menggunakan metode yang dijelaskan dalam literasi ini.

Kumpulan contoh persamaan dapat diperluas untuk mencakup konservasi energi dan model terkait konduksi panas dan kapasitas panas, yang dijelaskan dalam Bagian 2.15 – 2.18.

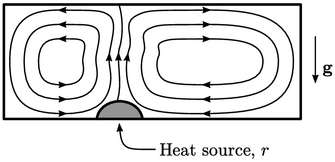
Himpunan persamaan massa, momentum dan energi dapat digabungkan untuk mensimulasikan konveksi alami, misalnya untuk aliran udara di sekitar ruangan. Dalam konveksi alami, suhu yang tidak seragam menyebabkan variasi kepadatan yang menghasilkan gaya terkait akibat gravitasi. Udara dingin terdorong ke bawah dan udara panas naik sehingga menciptakan daya apung. Variasi suhu yang kecil, seperti karena sumber panas $persamaan$ , dapat menyebabkan daya apung menjadi gaya yang dominan.

Persamaan perkiraan sederhana 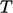$persamaan$ dapat diturunkan, dimulai dari konservasi energi dalam dalam bentuk Persamaan (2.57). Perkiraan viskositas konstan 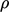$persamaan$ (dengan 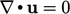$persamaan$ ) dan nol mengurangi syarat kerja tegangan/tekanan menjadi nol.

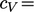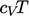Dengan asumsi $persamaan$ konstan, kita dapat menerapkan Persamaan (2.63), yang direduksi menjadi substitusi $persamaan$ karena $persamaan$ turunan dari konstanta 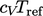$persam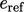aan$ dan $persamaan$ adalah nol. Menerapkan hukum Fourier Persamaan (2.54) mengarah ke;

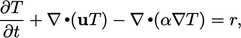@T- @t + r (uT) r ( rT ) = r; \relax \special {t4ht=

(2.65)

di mana difusivitas termal 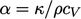dan menjadi sumber panas dalam satuan SI .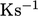

Ini adalah contoh lain, mirip dengan Persamaan (2.49), dari persamaan transportasi mengandung turunan waktu, adveksi, difusi dan sumber panas. Dengan menerapkan kondisi batas yang sesuai, persamaan tersebut dapat diselesaikan .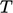

Kekuatan Apung (Bouyancy Force)

Efek daya apung dapat disimulasikan dengan mengatur gaya benda 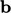dalam Persamaan (2.47) untuk fluida Newton yang tidak dapat dimampatkan. Meskipun asumsi 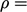konstanta diterapkan pada semua persamaan governing secara umum, konstanta asumsi tidak dapat diterapkan pada gaya ini. Oleh karena itu, menggunakan persamaan;

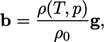$b = -(T;p)g; 0 \relax \special {t4ht=$

(2.66)

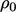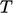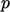di mana $persamaan$ adalah massa jenis pada keadaan referensi, misalnya pada titik awal $persamaan$ dan 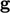$persamaan$ , dan $persamaan$ yang merupakan percepatan gravitasi.

Massa jenis 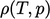$persamaan$ merupakan fungsi dari 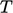$persamaan$ dan secara opsional 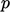$persamaan$ , disediakan oleh beberapa persamaan keadaan, misalnya persamaan gas ideal (2.55). Persamaan momentum akhir ini termasuk gaya apung, dan asumsi 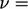$persamaan$ konstan adalah:

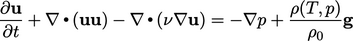@u (T;p) ---+ r (uu) r ( ru) = rp + ------g @t 0 \relax \special {t4ht=

(2.67)

Himpunan persamaan massa, momentum dan energi menjadi Persamaan (2.48), Persamaan (2.67), dan Persamaan (2.65), yang dapat digunakan untuk menyelesaikan aliran dengan konveksi alami.