16.11 Latihan
Latihan 1 Bagian dari sistem pasokan gas ditunjukkan pada Gambar 16.4. Rata aliran massa dalam bagian pipa diberikan oleh
di mana adalah penurunan tekanan sepanjang panjang bagian pipa,
adalah kepadatan gas, dan C adalah konduktivitas gas. Data berikut diketahui:
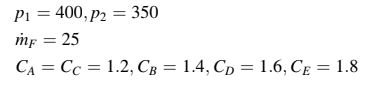
dengan kepadatan yang berkaitan dengan tekanan melalui Jika arah aliran adalah seperti yang ditunjukkan pada gambar, temukan
dan
dengan menggunakan prosedur berikut:
- Mulai dengan menebak untuk
dan
- Menghitung nilai
berdasarkan tekanan dan kepadatan yang diduga.
- Membangun persamaan tekanan-koreksi dan memecahkan untuk
dan
- Memperbarui tekanan dan nilai
Apakah Anda perlu mengulangi? Mengapa ya?
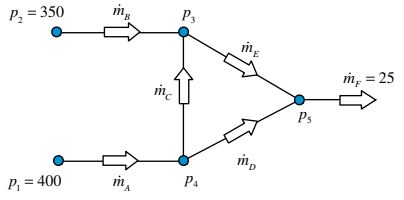
Gambar 16.4 Bagian dari sistem pasokan gas
Latihan 2 Pertimbangkan aliran gas ideal dalam pipa converging yang ditunjukkan pada Gambar 16.5, di mana masing-masing volume kontrol memiliki Area dari berbagai permukaan adalah
dengan
dan
Gambar 16.5 Konvergensi pipa
Arus area variabel dianggap satu dimensi dan isentropik. Pada inlet tekanan total adalah dan suhu stagnansi adalah To;
Pada output, tekanan statik adalah
Mengatur persamaan koreksi momentum dan tekanan untuk tiga volume kontrol dan mendapatkan nilai kecepatan, tekanan, kepadatan, dan suhu dimulai dengan bidang nilai yang seragam
(M adalah bilangan Mach)
dan
Lakukan 3 iterasi. Perhatikan bahwa tidak perlu memecahkan persamaan energi karena medan suhu dapat diekstrak dari kondisi suhu stagnansi konstan.
Latihan 3 Pertimbangkan arus dari gas ideal dalam pipa divergen yang ditunjukkan pada Gambar 16.6, di mana masing-masing volume kontrol memiliki Area dari berbagai permukaan adalah
dengan
dan
Gambar 16.6 Nozel melebar
Aliran area variabel diasumsikan sebagai satu dimensi dan isentropik. Pada inlet, tekanan total adalah jumlah Mach adalah
dan suhu adalah
Pada outlet, aliran tetap supersonik. Atur persamaan momentum dan koreksi tekanan untuk tiga volume kontrol dan peroleh nilai kecepatan, tekanan, kepadatan, dan suhu dimulai dengan lapangan nilai yang seragam
dan
Lakukan tiga iterasi. Perhatikan bahwa tidak perlu menyelesaikan persamaan energi karena lapangan suhu dapat diekstrak dari kondisi suhu stagnasi konstan.
Latihan 4 (OpenFOAM®)
Tentukan dalam solver simpleFoamCompressible variabel baru untuk jumlah Mach lokal yang akan divisualisasikan selama simulasi.
Latihan 5 (OpenFOAM®)
Modifikasi dalam kondisi batas totalPressureCorrectorComp, cara Eq. (16.44) diberlakukan, menggunakan sekarang fungsi nilaiInternalCoeffs() sambil mereset gradientInternal Coeffs(). (Petunjuk: lihat Bab 11 dan 19)
Latihan 6 (OpenFOAM®)
Periksa solver rhoSimpleFoam yang dapat ditemukan di $FOAM_SRC/../ applications/solvers/compressible/rhoSimplexFoam/pEqn.C dan bandingkan dengan algoritma yang dijelaskan dalam bab ini.
Latihan 7 (OpenFOAM®)
Kembangkan algoritma PISO yang dapat dimampatkan dan implementasikan mulai dari kode simpleFoamCompressible yang dijelaskan dalam bab ini.
