MENYELESAIKAN SUB-LAPISAN KENTAL
Fungsi dinding diperkenalkan di Sec. 7.5 untuk menghindari kebutuhan mesh besar dengan sel-sel yang cukup kecil untuk menyelesaikan lapisan batas menjadi sub-lapisan kental. Mereka memberikan prediksi yang masuk akal dengan 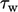 menggunakan hukum log untuk distribusi kecepatan di sub-lapisan inersia.
menggunakan hukum log untuk distribusi kecepatan di sub-lapisan inersia.

Sebagai alternatif, simulasi CFD dapat menggunakan jaring dengan sel yang cukup tipis untuk menyelesaikan aliran melalui sub-lapisan kental, misalnya dengan tinggi pusat sel dekat dinding yang sesuai dengan 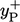 = 1, untuk prediksi yang lebih akurat
= 1, untuk prediksi yang lebih akurat 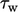 . Jika demikian, model turbulensi harus dapat berfungsi dengan baik di daerah aliran kental.
. Jika demikian, model turbulensi harus dapat berfungsi dengan baik di daerah aliran kental.
Model seperti ini biasanya digambarkan sebagai “bilangan Reynolds rendah”.Persamaan ini tidak mengacu pada 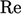 perhitungan aliran berdasarkan skala karakteristik permasalahan, misalnya kecepatan aliran rata-rata aksial dan diameter pipa. Sebaliknya, ini adalah bilangan Reynolds “turbulensi”
perhitungan aliran berdasarkan skala karakteristik permasalahan, misalnya kecepatan aliran rata-rata aksial dan diameter pipa. Sebaliknya, ini adalah bilangan Reynolds “turbulensi” 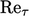 yang didasarkan pada skala kecepatan
yang didasarkan pada skala kecepatan 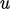 dan ukuran
dan ukuran 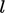 pusaran turbulen dan dapat didefinisikan sebagai
pusaran turbulen dan dapat didefinisikan sebagai
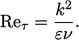 | (7.27) |
Definisi ini diperoleh dari argumen skala yang diperkenalkan di Bagian. 6.6, di mana 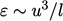 . Karena
. Karena 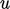 mewakili fluktuasi,
mewakili fluktuasi, 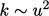 . Menggabungkan ekspresi ini ke dalam bilangan Reynolds menghasilkan Persamaan. (7.27).
. Menggabungkan ekspresi ini ke dalam bilangan Reynolds menghasilkan Persamaan. (7.27).
Konsistensi asimtotik
Model turbulensi rendah 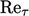 memperhatikan perilaku fluktuasi kecepatan, misalnya
memperhatikan perilaku fluktuasi kecepatan, misalnya 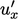 ,
, 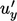 dalam batas
dalam batas 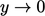 batas padat.
batas padat.
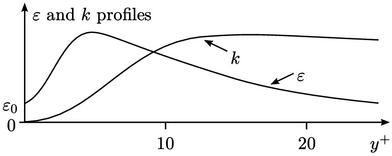
Mereka bertujuan untuk menangkap bentuk, profil, 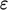 dan
dan 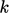 saat mereka mendekat
saat mereka mendekat 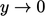 . Tentukan
. Tentukan 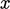 dan
dan 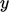 tentukan masing-masing arah tangensial dan tegak lurus dinding. Profil fluktuasi kecepatan dapat dinyatakan dengan polinomial dalam
tentukan masing-masing arah tangensial dan tegak lurus dinding. Profil fluktuasi kecepatan dapat dinyatakan dengan polinomial dalam 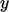 , yaitu
, yaitu
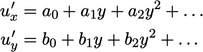
di mana 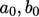 , dll. adalah fungsi ruang dan waktu. Kondisi tidak ada slip menyiratkan
, dll. adalah fungsi ruang dan waktu. Kondisi tidak ada slip menyiratkan 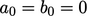 , jadi
, jadi 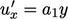 ke urutan terendah di
ke urutan terendah di 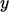 . Sebab
. Sebab 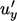 , sejak itu
, sejak itu 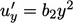 , di dinding,
, di dinding, 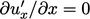 dan secara kontinuitas
dan secara kontinuitas 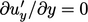 .
.
Sifat-sifat turbulen, pada orde terendah di 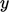 , adalah sebagai berikut.
, adalah sebagai berikut.
- Dari Detik. 6.11,
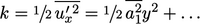
- Dari Persamaan. (6.30),
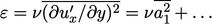
Oleh karena itu model mencapai konsistensi asimtotik ketika
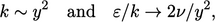 | (7.28) |
dalam batas itu 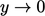 .
.
