10.3.2 Metode Gauss-Seidel
Pendekatan yang lebih populer terhadap metode Jacobi adalah metode Gauss-Seidel, yang memiliki karakteristik konvergensi yang lebih baik. Ini sedikit lebih hemat memori karena tidak memerlukan penyimpanan perkiraan baru dalam array terpisah. Sebaliknya, metode ini menggunakan perkiraan terbaru yang tersedia daridalam perhitungannya. Formula iteratif dalam metode Gauss-Seidel, yang ditampilkan secara skematis dalam Gambar 10.3, diberikan sebagai
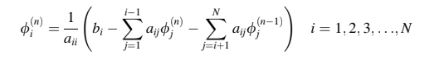
Dalam bentuk matriks, Persamaan (10.76) dituliskan sebagai
Secara efektif, metode Gauss-Seidel menggunakan nilai-nilai paling baru dalam iterasinya, khususnya semua nilai untuk j < i karena pada saat
akan dihitung, nilai-nilai
pada iterasi saat ini sudah dihitung. Pendekatan ini juga menghemat memori karena nilai yang lebih baru selalu menimpa nilai sebelumnya. Iterasi Gauss-Seidel akan konvergen selama,
Meskipun dalam beberapa kasus metode Jacobi konvergen lebih cepat, Gauss-Seidel adalah metode yang lebih disukai.
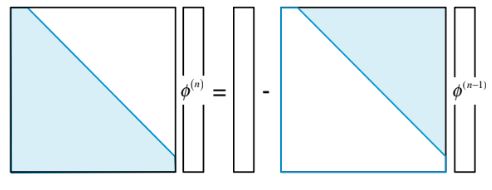
Gambar 10.3 Representasi grafis dari metode Gauss-Seidel
