4.9 Mixed Fixed Value Gradient

4.9 mixed fixed value gradient

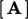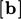Mixed fixed value gradient. Detik. 4.8 diakhiri dengan tabel faktor kontribusi terhadap koefisien dan nilai tetap $persamaan$ serta $persamaan$ kondisi batas gradien tetap.

Ini membedakan antara kontribusi untuk diskritisasi suku adveksi yang memerlukan nilai pada permukaan, dan suku Laplacian yang memerlukan gradien normal .

Kondisi nilai/gradien tetap campuran ditentukan dengan memperkenalkan pecahan nilai $persamaan$ yang mana

Dalam rentang tersebut, 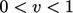$persamaan$ kondisi beroperasi di antara nilai tetap dan gradien tetap. Kondisi campuran secara sederhana diimplementasikan dengan memadukan nilai tetap dan kontribusi gradien tetap sebesar $persamaan$ , seperti yang ditunjukkan pada tabel di bawah.

Kondisi campuran ini memberikan kerangka untuk kondisi batas yang dapat beralih antara nilai tetap 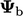dan gradien tetap 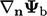, dengan cara mengubah . Peralihan sering kali didasarkan pada arah aliran, 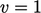sesuai dengan aliran masuk dan 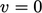aliran keluar.

Beberapa kondisi batas dapat beroperasi pada rentang pecahan nilai 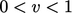. Kondisi Robin, yang dijelaskan selanjutnya, juga dapat dinyatakan sebagai kondisi campuran dengan variasi .

Kondisi Robin

Kondisi Robin⁵ menggabungkan nilai dan gradien normal pada batas melalui ekspresi:

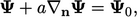$+ arn = 0; \relax \special {t4ht=$

(4.10)

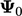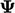di mana $persamaan$ adalah koefisien skalar dengan satuan panjang dan $persamaan$ merupakan nilai konstan dari $persamaan$ .

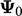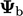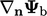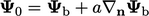Kondisi Robin dapat diperlakukan seperti kondisi campuran dengan menghubungkannya $persamaan$ dengan nilai tetap referensi $persamaan$ dan gradien $persamaan$ pada suatu batas, menurut $persamaan$ .

Mengganti 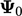$persamaan$ dalam Persamaan. (4.10) dan menjadikan 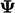$persamaan$ subjek persamaan menghasilkan:

Perbandingan dengan faktor nilai pada tabel sebelumnya menunjukkan bahwa kondisi Robin sesuai dengan kondisi campuran dengan pecahan nilai 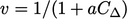$persamaan$ .

Dalam bentuk ini, 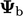$persam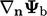aan$ dan $persamaan$ berhubungan dengan limit 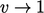$persam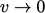aan$ dan $persamaan$ , masing-masing. Nilai dapat dipilih dalam batas ini untuk mewakili kondisi fisika.

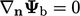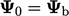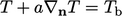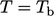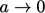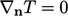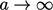Dalam banyak kasus, gradien referensi $persamaan$ sedemikian rupa sehingga $persamaan$ dalam Persamaan. (4.10). Misalnya suatu kondisi suhu $persamaan$ akan cenderung $persamaan$ sebagai $persamaan$ dan $persamaan$ sebagai $persamaan$ .

Pecahan nilai $persamaan$ mencakup $persamaan$ , sehingga kondisi beroperasi “di tengah” antara nilai tetap dan gradien jika $persamaan$ besarannya sama dengan tinggi sel batas.