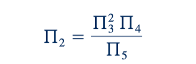Penentuan Suku Pi dengan Inspeksi
Metode pengulangan variabel untuk membentuk pi terms telah disajikan dalam Bagian 7.3. Metode ini menyediakan prosedur langkah demi langkah yang, jika dilaksanakan dengan benar, akan memberikan seperangkat pi terms yang benar dan lengkap. Meskipun metode ini sederhana dan langsung, namun agak membosankan, terutama untuk masalah yang melibatkan jumlah variabel yang besar. Karena satu-satunya batasan yang diberlakukan pada pi terms adalah bahwa mereka harus 112 benar dalam jumlah, 122 tanpa dimensi, dan 132 independen, maka memungkinkan untuk hanya membentuk pi terms dengan inspeksi, tanpa harus menggunakan prosedur yang lebih formal. Untuk mengilustrasikan pendekatan ini, kita akan kembali mempertimbangkan penurunan tekanan per satuan panjang sepanjang pipa halus. Terlepas dari teknik yang digunakan, titik awalnya tetap sama yaitu menentukan variabel-variabel, yang dalam hal ini adalah
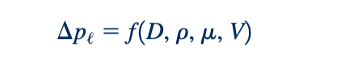
Selanjutnya, dimensi dari variabel-variabel tersebut adalah:
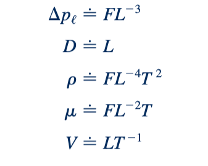
Kemudian, jumlah dimensi referensi ditentukan. Penerapan teorema pi kemudian memberi tahu kita berapa banyak pi term yang dibutuhkan. Dalam masalah ini, karena ada lima variabel dan tiga dimensi referensi, dua pi term diperlukan. Dengan demikian, jumlah pi term yang dibutuhkan dapat dengan mudah diperoleh. Penentuan jumlah ini harus selalu dilakukan pada awal analisis.
Setelah jumlah pi term diketahui, kita dapat membentuk setiap pi term melalui inspeksi, hanya dengan menggunakan fakta bahwa setiap pi term harus tak berdimensi. Kita akan selalu membiarkan Π1 berisi variabel dependen, yang dalam contoh ini adalah ∇𝜌ℓ. Karena variabel ini memiliki dimensi FL^(-3), kita perlu menggabungkannya dengan variabel lain sehingga produk tanpa dimensi akan dihasilkan. Salah satu kemungkinannya adalah dengan membagi ∇𝜌ℓ dengan 𝜌 sehingga
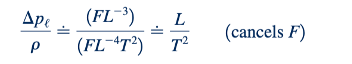
Ketergantungan pada F telah dihilangkan, tetapi ∇𝜌ℓ/𝜌 jelas tidak berdimensi. Untuk menghilangkan ketergantungan pada T, kita dapat membagi dengan V^2 sehingga
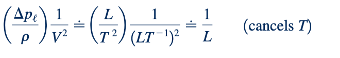
Akhirnya, untuk membuat kombinasi tersebut adimensi, kita mengalikannya dengan D sehingga
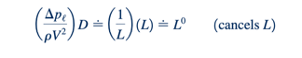
Dengan demikian,
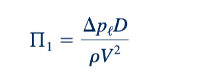
Selanjutnya, kita akan membentuk pi term kedua dengan memilih variabel yang tidak digunakan dalam Π1, yang dalam hal ini adalah 𝜇. Kita cukup menggabungkan 𝜇 dengan variabel lain untuk membuat kombinasi tersebut adimensi (tapi jangan gunakan ∇𝜌ℓ dalam Π2, karena kita ingin variabel tergantung hanya muncul di Π2). Sebagai contoh, bagi 𝜇 dengan p (untuk menghilangkan F), kemudian bagi dengan V (untuk menghilangkan T), dan akhirnya bagi dengan D (untuk menghilangkan L). Dengan demikian,

dan maka dari itu,

dan, tentu saja, hasilnya sama dengan yang kita peroleh dengan menggunakan metode variabel berulang.
Perhatian tambahan, ketika kita membentuk pi term dengan cara inspeksi, adalah pastikan bahwa mereka semua independen. Pada contoh aliran pipa, Π2 mengandung 𝜇, yang tidak muncul di Π1, dan oleh karena itu dua pi term ini jelas independen. Dalam kasus yang lebih umum, suatu pi term tidak akan independen dari yang lain dalam masalah yang diberikan jika dapat dibentuk oleh beberapa kombinasi dari yang lain. Misalnya, jika Π2 dapat dibentuk oleh kombinasi dari misalnya Π3, Π4, dan Π5 seperti