perpindahan panas dalam aliran turbulen

Fokus awal pemodelan turbulensi adalah untuk menangkap pengaruh pencampuran terhadap difusi momentum karena hal ini mempengaruhi solusi aliran secara keseluruhan. Namun sifat-sifat lain juga terbawa oleh gerakan pusaran turbulen, khususnya panas.

Pengaruh turbulensi terhadap perpindahan panas dapat dijelaskan menggunakan persamaan energi dalam berikut , yang diperoleh dengan mensubstitusikan turunan material ke dalam Persamaan. (2.57) dan mengabaikan :

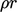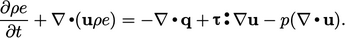$@ e ----+ r (u e) = r q + ☐☐☐ ru p(r u): @t \relax \special {t4ht=$

(7.44)

Dalam aliran turbulen, energi internal dapat diuraikan menjadi komponen rata-rata dan berfluktuasi 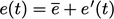, lihat Persamaan. (6.11). Rata-rata ansambel dari suku-suku dalam memperkenalkan fluks panas

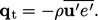$---- qt = u0e0: \relax \special {t4ht=$

(7.45)

Fluks panas tambahan inidalam persamaan energi setara dengan tegangan Reynolds 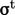, Persamaan. (6.14), dalam momentumnya. Boussinesq dimodelkan 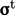oleh Persamaan. (6.20), menggunakan konsep viskositas pusaran air 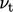yang berhubungan dengan pencampuran turbulen, analog dengan viskositas akibat gerak molekul menurut persamaan hukum Newton. (2.41).

Demikian pula 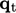dapat dimodelkan dengan menggunakan konduktivitas termal turbulen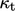karena pencampuran turbulen, dengan analogi dengan hukum Fourier Persamaan. (2.54) untuk konduksi karena interaksi molekul

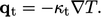$q = rT: t t \relax \special {t4ht=$

(7.46)

Fluks panas total 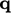dalam Persamaan. (7.44) kemudian dinyatakan dalam gabungan pencampuran turbulen dan interaksi molekul, menggunakan konduktivitas termal efektif 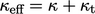, sebagai berikut:

$q = rT: eﬀ \relax \special {t4ht=$

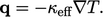(7.47)

Memodelkan perpindahan panas turbulen

Perpindahan panas turbulen dapat dimasukkan ke dalam model turbulensi berdasarkan viskositas eddy dan rata-rata Reynolds, dengan fungsi dinding termal tambahan.

Pertama, perhitungan 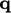dengan Persamaan. (7.47) membutuhkan 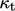dari model turbulensi. Pendekatan umum untuk menghitung 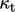adalah 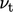berdasarkan perkiraan bilangan Prandtl yang bergejolak

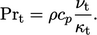$-t Prt = cp t: \relax \special {t4ht=$

(7.48)

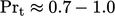memberikan perkiraan yang baik untuk banyak fluida, dan 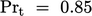sering kali dipilih sebagai nilai default untuk perhitungan CFD. Untuk beberapa fluida yang tidak biasa, misalnya logam cair, .

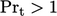Fluks panas dinding

Perhitungan perpindahan panas melalui dinding batas merupakan aspek penting dari banyak simulasi CFD. Di dekat tembok, sebarannya 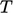cenderung meniru .

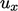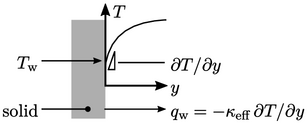
$GAMBAR\santai \khusus {t4ht=$

Akibatnya, tantangan dalam menghitung fluks panas dinding 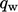serupa dengan tegangan geser dinding 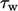. Sel yang dekat dengan dinding harus sangat tipis untuk menyelesaikan sublapisan kental di 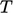(kapan ).

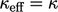Jika tidak, fungsi dinding dapat digunakan untuk menyesuaikan guna 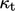mengkompensasi rendahnya prediksi 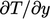seperti yang dijelaskan dalam Bagian. 7.14.