Persamaan Bernoulli
Dalam Bagian 3.2, persamaan Bernoulli diturunkan dengan menerapkan langsung hukum kedua Newton pada partikel fluida yang bergerak sepanjang garis aliran. Dalam bagian ini, kita akan kembali menurunkan ini penting.

persamaan, dimulai dari persamaan Euler. Tentu saja, kita seharusnya mendapatkan hasil yang sama karena persamaan Euler hanya merupakan pernyataan dari hukum kedua Newton yang diungkapkan dalam bentuk umum yang berguna untuk masalah aliran dan mempertahankan batasan viskositas nol. Kita akan membatasi perhatian kita pada aliran yang mantap sehingga persamaan Euler dalam bentuk vektor menjadi
Kita ingin mengintegrasikan persamaan diferensial ini sepanjang garis aliran sembarang. Kita akan memilih sistem koordinat dengan sumbu z vertikal (dengan arah "atas" positif), sehingga, seperti yang ditunjukkan oleh gambar di samping, vektor percepatan gravitasi dapat diekspresikan sebagai


di mana g adalah magnitudo dari vektor percepatan gravitasi. Selain itu, akan berguna untuk menggunakan identitas vektor,
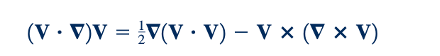
Persamaan 6.53 sekarang dapat dituliskan dalam bentuk:

dan persamaan ini dapat diubah urutannya untuk menghasilkan:

Kemudian kita ambil hasil kali titik dari setiap suku dengan panjang diferensial ds sepanjang garis arus (Gambar 6.12). Dengan demikian,
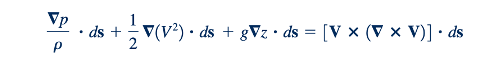
Karena ds memiliki arah sepanjang garis arus, vektor ds dan V adalah sejajar. Namun, seperti yang ditunjukkan oleh gambar di pinggiran halaman, vektor 𝑉 𝑥 (∇ 𝑥 𝑉) tegak lurus terhadap V (mengapa?), jadi dapat disimpulkan bahwa

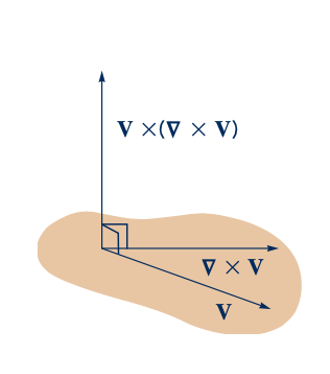
Selain itu, ingatlah bahwa hasil kali titik antara gradien suatu skalar dan panjang diferensial memberikan perubahan diferensial dalam skalar tersebut dalam arah panjang diferensial. Artinya, dengan ds = dxˆidyjˆdzkˆ, kita dapat menulis ∇p. ds = (𝜕p/𝜕x) dx + (𝜕p/𝜕y)dy + (𝜕p/𝜕z)dz = dp. Dengan demikian, Persamaan 6.54 menjadi
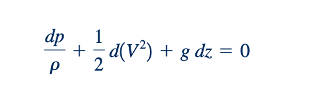
dimana perubahan p, V, dan z terjadi sepanjang garis arus. Persamaan 6.55 sekarang dapat diintegrasikan untuk menghasilkan
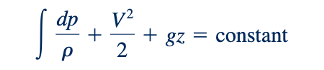
Persamaan 6.56 menunjukkan bahwa jumlah dari tiga suku di sisi kiri persamaan harus tetap konstan sepanjang garis aliran tertentu. Persamaan 6.56 berlaku baik untuk fluida yang dapat dimampatkan maupun yang tidak dapat dimampatkan.aliran inviskid, tetapi untuk fluida yang dapat dimampatkan, variasi ρ dengan p harus ditentukan sebelum suku pertama dalam Persamaan 6.56 dapat dievaluasi
Untuk fluida inviskid, tak dapat dimampatkan (umumnya disebut sebagai fluida ideal), Persamaan 6.56 dapat ditulis sebagai:

dan persamaan ini adalah persamaan Bernoulli yang digunakan secara luas di Bab 3. Seringkali nyaman untuk menuliskan Persamaan 6.57 antara dua titik (1) dan (2) sepanjang garis aliran dan untuk mengekspresikan persamaan dalam bentuk "head" dengan membagi setiap suku dengan g sehingga

