REFORMULATING HO SCHEMES IN TERMS OF GRADIENTS
Pendekatan ini bergantung pada profil yang dikembangkan di atas grid terstruktur dan dapat dijelaskan dengan baik dengan menuliskan ulang skema QUICK [2] menggunakan terminologi baru, kemudian menggeneralisasi hasil untuk setiap profil orde kedua yang dikembangkan menggunakan tiga titik. Hubungan fungsional dari skema QUICK [2] dapat ditulis sebagai
Dengan mendekati gradien di lokasi C dan f dalam arah dCF atau ζ seperti yang ditunjukkan dalam Gambar 11.19, maka gradien di pusat-pusat C dan f dihitung sebagai:
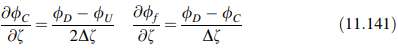
Dengan menggunakan Persamaan (11.141), Persamaan (11.140) dapat dirumuskan kembali menjadi:
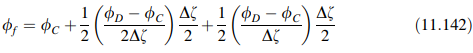
atau
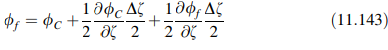
Dengan menunjukkan vektor antara C dan f dengan dCf, dalam bentuk vektor persamaan di atas menjadi:
yang sangat sesuai untuk digunakan dalam konteks grid yang tidak terstruktur karena hanya memerlukan informasi terkait gradien di lokasi C dan f. Selama perhitungan gradien ini akurat hingga orde kedua, cara perhitungannya menjadi tidak penting. Ini memberikan fleksibilitas yang lebih tinggi, dibandingkan dengan formulasi asli, pada grid yang tidak terstruktur. Selain itu, Persamaan (11.144) menyarankan bahwa sebuah profil berdasarkan tiga titik dapat dituliskan sebagai:
di mana konstanta a, b, dan c ditentukan dengan menyamakan ϕf dengan profil yang diperoleh dari grid terstruktur. Bentuk terdiscretisasi umum dari Persamaan (11.145) dapat ditemukan sekali, kemudian digunakan dalam semua turunan berikutnya. Ini dihasilkan dengan pertama-tama mensubstitusi nilai perkiraan gradien menggunakan Persamaan (11.141) untuk menghasilkan:
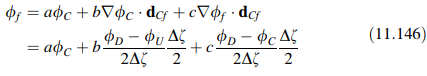
dan setelah beberapa manipulasi aljabar, bentuk akhirnya diperoleh sebagai:
Dengan menggunakan persamaan di atas, perhitungan koefisien a, b, dan c dapat dengan mudah dilakukan. Sebagai contoh, profil SOU dalam hal gradien dapat ditemukan sebagai berikut:
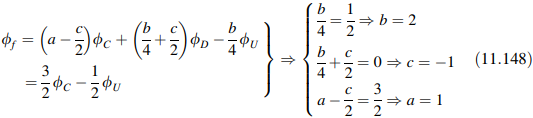
Dengan demikian, bentuk setara dari skema SOU diberikan oleh:
Mengikuti prosedur yang sama, bentuk gradien dari skema-skema yang telah disajikan sebelumnya ditemukan sebagai berikut:
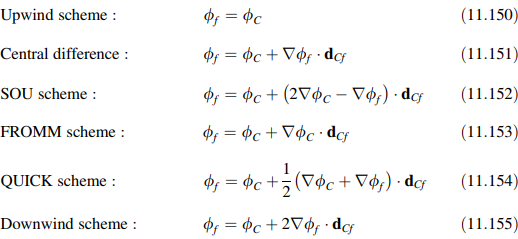
Sebuah bab lengkap didedikasikan untuk perhitungan gradien di pusat elemen dan wajah, dan pembaca disarankan untuk merujuk ke Bab 9 untuk perhitungan ∇ϕC dan ∇ϕf.
