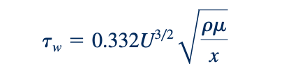Solusi Lapisan Batas Prandtl/Blasius
Secara teori, rincian aliran kental dan tak terkompresibel di sekitar objek apa pun dapat diperoleh dengan memecahkan persamaan Navier-Stokes yang mengatur yang dibahas di Bagian 6.8.2. Untuk aliran laminar dua dimensi yang stabil dengan efek gravitasi yang dapat diabaikan, persamaan ini (Eqs. 6.127a, b, dan c) disederhanakan menjadi yang berikut:
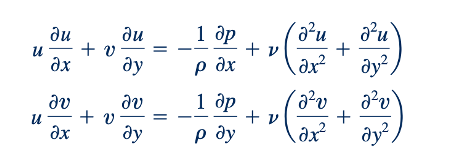
yang menyatakan hukum kedua Newton. Selain itu, persamaan konservasi massa, Eq. 6.31, untuk aliran tak terkompresibel adalah:
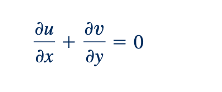
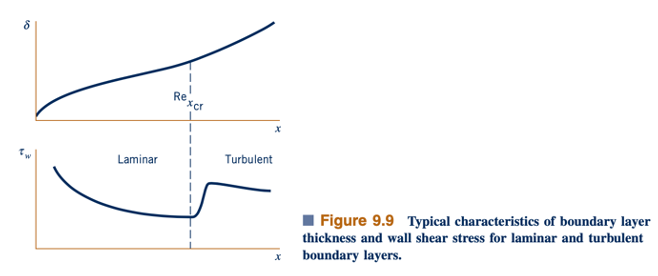
Kondisi batas yang sesuai adalah bahwa kecepatan fluida jauh dari benda adalah kecepatan aliran hulu dan bahwa fluida melekat pada permukaan benda padat. Meskipun masalah matematis ini terdefinisi dengan baik, belum ada yang berhasil mendapatkan solusi analitis untuk persamaan ini untuk aliran melewati benda berbentuk apa pun! Saat ini banyak pekerjaan dilakukan untuk mendapatkan solusi numerik untuk persamaan-persamaan ini untuk berbagai geometri aliran.
Pada beberapa asumsi (berlaku untuk aliran dengan jumlah Reynolds besar) diterapkan oleh Prandtl untuk menyederhanakan persamaan-persamaan yang mengatur. Pada tahun 1908, salah satu mahasiswa Prandtl, H. Blasius, berhasil menyelesaikan persamaan-persamaan yang disederhanakan ini untuk aliran lapis batas melintasi plat datar sejajar dengan arus. Berikut adalah gambaran singkat tentang teknik ini dan hasilnya. Detail tambahan dapat ditemukan dalam literatur (Ref. 1–32).
Karena lapisan batas tipis, diharapkan bahwa komponen kecepatan yang tegak lurus terhadap plat jauh lebih kecil daripada yang sejajar dengan plat dan bahwa laju perubahan setiap parameter melintasi lapisan batas seharusnya jauh lebih besar daripada sepanjang arah aliran. Itu artinya,
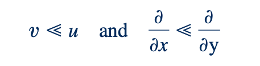
Secara fisik, aliran secara utama sejajar dengan plat dan setiap sifat fluida diadvak downstream jauh lebih cepat daripada penyebarannya melintasi garis arus.
Dengan asumsi-asumsi ini, dapat ditunjukkan bahwa persamaan-persamaan yang mengatur (Eqs. 9.5, 9.6, dan 9.72) menyederhanakan menjadi persamaan-persamaan lapisan batas berikut:
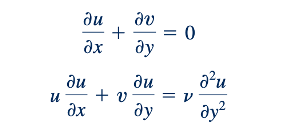
Meskipun kedua persamaan lapisan batas ini dan persamaan Navier-Stokes asli adalah persamaan diferensial parsial nonlinear, ada perbedaan yang signifikan di antara keduanya. Pertama, persamaan momentum y telah dihilangkan, hanya meninggalkan persamaan kontinuitas asli, tidak terubah, dan persamaan momentum x yang dimodifikasi. Salah satu variabel, tekanan, telah dihilangkan, hanya meninggalkan komponen kecepatan x dan y sebagai tidak diketahui. Untuk aliran lapisan batas di atas plat datar, tekanan konstan di seluruh fluida. Aliran tersebut mewakili keseimbangan antara efek viscous dan inersia, dengan tekanan tidak memainkan peran apa pun.
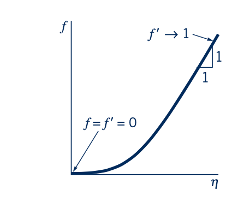
Seperti yang ditunjukkan oleh gambar di pinggir, syarat batas untuk persamaan lapisan batas yang mengatur adalah bahwa fluida melekat pada plat.
dan bahwa di luar lapisan batas aliran adalah aliran uniform di hulu u = U. Itu adalah,
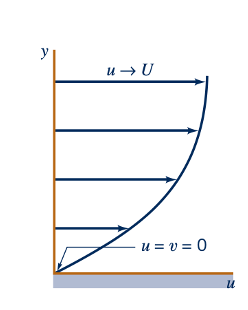
Dalam istilah matematis, kecepatan hulu dihampiri secara asimtotik saat menjauh dari plat. Secara fisik, kecepatan aliran berada dalam 1% dari kecepatan hulu pada jarak 𝛿 dari plat.
Secara matematis, persamaan Navier–Stokes (Eqs. 9.5 dan 9.62) dan persamaan kontinuitas (Eq. 9.72) adalah persamaan elips, sedangkan persamaan untuk aliran lapisan batas (Eqs. 9.8 dan 9.92) adalah persamaan parabola. Karakter solusi dari dua set persamaan ini, oleh karena itu, berbeda. Secara fisik, fakta ini mengartikan gagasan bahwa apa yang terjadi di hulu dari suatu lokasi tertentu dalam lapisan batas tidak dapat mempengaruhi apa yang terjadi di hulu dari titik tersebut. Artinya, apakah plat yang ditunjukkan dalam Gambar 9.5c berakhir dengan panjang ℓ atau diperpanjang menjadi panjang 2ℓ, aliran dalam segmen pertama dengan panjang ℓ akan sama. Selain itu, keberadaan plat tidak memiliki efek pada aliran di depan plat. Di sisi lain, keelipan memungkinkan informasi aliran untuk merambat ke segala arah, termasuk hulu.
Secara umum, solusi dari persamaan diferensial parsial nonlinear (seperti persamaan lapisan batas, Eqs. 9.8 dan 9.92) sangat sulit untuk diperoleh. Namun, dengan menerapkan transformasi koordinat cerdik dan perubahan variabel, Blasius mengurangi persamaan diferensial parsial menjadi bentuk differential biasa yang berhasil ia selesaikan. Deskripsi singkat tentang proses ini diberikan di bawah ini. Rincian tambahan dapat ditemukan dalam buku-buku standar yang membahas aliran lapisan batas.
Dapat diperdebatkan bahwa dalam bentuk tak berdimensi, profil kecepatan lapisan batas pada plat datar seharusnya mirip terlepas dari lokasi sepanjang plat. Artinya,
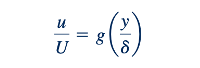
di mana g(𝑦/𝛿) adalah fungsi yang belum diketahui yang akan ditentukan. Selain itu, dengan menerapkan analisis orde besaran dari gaya yang bertindak pada fluida dalam lapisan batas, dapat ditunjukkan bahwa ketebalan lapisan batas berkembang sebagai akar kuadrat dari 𝑥 dan berbanding terbalik dengan akar kuadrat dari 𝑈. Artinya,
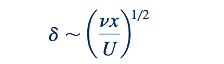
Kesimpulan tersebut berasal dari keseimbangan antara gaya viscous dan inersial dalam lapisan batas dan dari fakta bahwa kecepatan bervariasi jauh lebih cepat dalam arah melintasi lapisan batas daripada sepanjangnya.
Oleh karena itu, kita memperkenalkan variabel kesamaan berdimensi 𝜂=(𝑈/𝑣𝑥)1/2 dan fungsi aliran 𝜓=(𝑣 𝑥 𝑈)1/2𝑓(𝜂) , di mana f= 𝑓(𝜂) adalah fungsi yang tidak diketahui. Ingat dari Bagian 6.2.3 bahwa komponen kecepatan untuk aliran dua dimensi diberikan dalam istilah fungsi aliran sebaga 𝑢=𝜕𝜓/𝜕𝑦 dan 𝑣=−𝜕𝜓/𝜕𝑥, yang untuk aliran ini menjadi
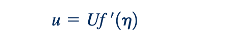
Dan
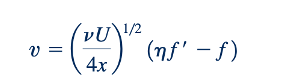
dengan notasi ( )'= d/d𝜂. Kita substitusikan Persamaan 9.12 dan 9.13 ke dalam persamaan-persamaan pemimpin, Persamaan 9.8 dan 9.9, untuk memperoleh (setelah manipulasi yang cukup) persamaan diferensial orde ketiga berikut:
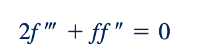
Seperti yang ditunjukkan oleh gambar di pinggir, kondisi batas yang diberikan dalam Persamaan 9.10 dan 9.11 dapat dituliskan sebagai

Persamaan diferensial parsial asli dan kondisi batas telah direduksi menjadi persamaan diferensial biasa dengan menggunakan variabel kesamaan 𝜂. Dua variabel independen, x dan y, digabungkan menjadi variabel kesamaan dengan cara yang mengurangi persamaan diferensial parsial dan kondisi batas menjadi persamaan diferensial biasa. Jenis reduksi ini tidak umumnya mungkin dilakukan. Sebagai contoh, metode ini tidak berfungsi pada persamaan Navier-Stokes lengkap, meskipun berfungsi pada persamaan lapisan batas.
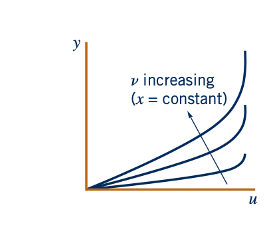
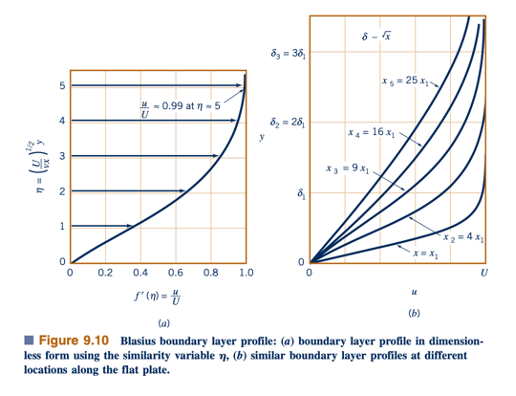
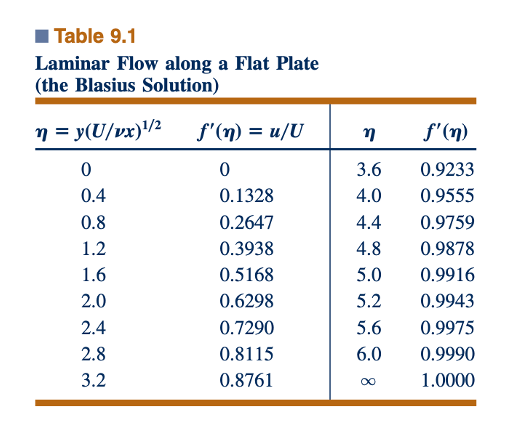
Meskipun tidak ada solusi analitis yang diketahui untuk Persamaan 9.14, relatif mudah untuk mengintegrasikan persamaan ini pada komputer. Profil lapis batas tanpa dimensi, u/U = f'(𝜂), yang diperoleh dengan solusi numerik dari Persamaan 9.14 (yang disebut solusi Blasius), digambarkan dalam Fig. 9.10a dan ditampilkan dalam Tabel 9.1. Profil kecepatan pada lokasi x yang berbeda mirip dalam arti bahwa hanya ada satu kurva yang diperlukan untuk menggambarkan kecepatan di setiap titik dalam lapisan batas. Karena variabel kesamaan h mengandung baik x maupun y, dari Fig. 9.10b terlihat bahwa profil kecepatan aktual adalah fungsi dari baik x maupun y. Profil pada lokasi x1 sama dengan yang pada x2 kecuali bahwa koordinat y diperpanjang dengan faktor (x1/x2)1/2. Anda dapat mencapai perubahan serupa dalam profil kecepatan lapis batas dengan mengubah viskositas kinematik, v, seperti yang ditunjukkan oleh gambar di pinggiran halaman.
Dari solusi ini, ditemukan bahwa u/U ≈0,99 ketika 𝜂 = 5,0. Dengan demikian,
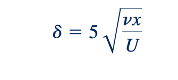
Atau
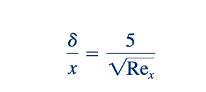
dimana Re x=Ux/v . Juga dapat ditunjukkan bahwa ketebalan pergeseran dan momentum diberikan oleh
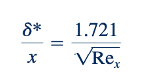
Dan
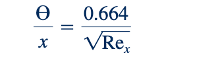
Dugaan tersebut adalah bahwa lapisan batas tipis jika Rex besar (yaitu, 𝛿 /𝑥→0 saat 𝑅𝑒𝑥→∞)
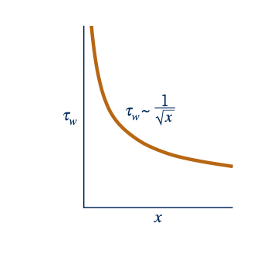
Dengan profil kecepatan yang diketahui, menentukan tegangan geser dinding, τw = 𝜇(𝜕𝑢/𝜕𝑦)𝑦=0, dimana gradien kecepatan dievaluasi pada pelat. Nilai ∂u/∂y pada y=0 dapat diperoleh dari solusi Blasius untuk memberikan