Struktur dan Ketebalan Lapisan Batas pada Pelat Datar
Ada beragam dalam ukuran lapisan batas dan struktur aliran di dalamnya. Sebagian dari variasi ini disebabkan oleh bentuk objek di mana lapisan batas terbentuk. Pada bagian ini, kita pertimbangkan situasi yang paling sederhana, di mana lapisan batas terbentuk pada plat datar yang tak terhingga panjang di mana mengalir fluida viscous yang tak dapat dipadatkan seperti yang ditunjukkan dalam Gambar 9.7. Jika permukaan tersebut melengkung (misalnya, sebuah silinder berbentuk lingkaran atau sebuah airfoil), struktur lapisan batas akan lebih kompleks. Aliran-aliran tersebut dibahas dalam Bagian 9.2.6.
Jika jumlah Reynolds cukup besar, hanya fluida di dalam lapisan batas yang relatif tipis pada plat yang akan merasakan efek plat tersebut. Artinya, kecuali di daerah sebelah plat, kecepatan aliran akan secara esensial menjadi V = Ui, kecepatan hulu. Untuk plat datar yang tak terhingga panjang yang membentang dari x = 0 hingga x = ∞, tidak jelas bagaimana mendefinisikan jumlah Reynolds karena tidak ada panjang karakteristik. Plat tersebut tidak memiliki ketebalan dan tidak memiliki panjang yang terbatas!
Untuk plat dengan panjang yang terbatas, jelas bahwa panjang plat, ℓ, dapat digunakan sebagai panjang karakteristik. Untuk plat tak terhingga panjang kita menggunakan x, jarak koordinat sepanjang plat dari tepi depan, sebagai panjang karakteristik dan mendefinisikan jumlah Reynolds sebagai Rex = Ux/n. Dengan demikian, untuk
Untuk setiap fluida atau kecepatan hulu, jumlah Reynolds akan cukup besar untuk aliran tipe lapisan batas (misalnya, seperti pada Gambar 9.5c) jika plat cukup panjang. Secara fisik, ini berarti situasi aliran yang diilustrasikan dalam Gambar 9.5 bisa dianggap terjadi pada plat yang sama tetapi harus dilihat dengan melihat bagian plat yang lebih panjang saat kita menjauh dari plat untuk melihat aliran dalam Gambar 9.5a, 9.5b, dan 9.5c, secara berturut-turut.
Jika plat cukup panjang, jumlah Reynolds Re = Uℓ/ν cukup besar sehingga aliran mengambil karakter lapisan batasnya (kecuali sangat dekat dengan tepi depan). Detail medan aliran di dekat tepi depan hilang bagi mata kita karena kita berdiri begitu jauh dari plat sehingga kita tidak dapat melihat detail-detail tersebut. Pada skala ini (Gambar 9.5c), plat memiliki pengaruh yang tidak signifikan pada fluida di depan plat. Kehadiran plat hanya terasa pada lapisan batas yang relatif tipis dan daerah ekor. Seperti yang pernah disebutkan, Prandtl pada tahun 1904 adalah yang pertama kali menghipotesiskan konsep tersebut. Ini telah menjadi salah satu titik balik utama dalam analisis mekanika fluida.
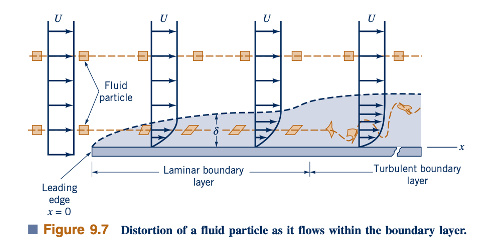
Pemahaman yang lebih baik tentang struktur aliran lapisan batas dapat diperoleh dengan mempertimbangkan apa yang terjadi pada partikel fluida yang mengalir ke dalam lapisan batas. Seperti yang ditunjukkan dalam Gambar 9.7, sebuah partikel kecil berbentuk persegi panjang mempertahankan bentuk aslinya saat mengalir dalam aliran seragam di luar lapisan batas. Setelah memasuki lapisan batas, partikel mulai terdistorsi karena gradien kecepatan dalam lapisan batas—bagian atas partikel memiliki kecepatan yang lebih besar dari pada bagian bawahnya. Partikel fluida tidak berputar saat mengalir di luar lapisan batas, tetapi mereka mulai berputar setelah melewati permukaan lapisan batas fiktif dan memasuki dunia aliran viscous. Aliran dikatakan irrotasional di luar lapisan batas dan rotasional di dalam lapisan batas. Dalam hal kinematika partikel fluida sebagaimana dibahas di Bagian 6.1, aliran di luar lapisan batas memiliki vortisitas nol, dan aliran di dalam lapisan batas memiliki vortisitas non-nol.
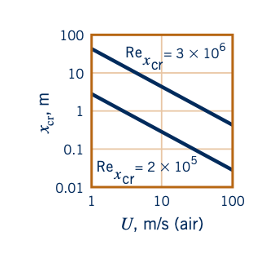
Pada jarak tertentu di sepanjang hilir dari leading edge, aliran lapisan batas menjadi turbulen dan partikel fluida menjadi sangat terdistorsi karena sifat turbulensi yang acak dan tidak teratur. Salah satu fitur khas aliran turbulen adalah terjadinya pencampuran yang tidak teratur dari partikel-fluida yang berukuran mulai dari partikel-fluida terkecil hingga yang sebanding dengan ukuran objek yang diminati. Untuk aliran laminar, pencampuran hanya terjadi pada skala molekuler. Skala molekuler ini memiliki ukuran yang jauh lebih kecil dari pada ukuran tipikal untuk pencampuran aliran turbulen. Transisi dari lapisan batas laminar menjadi lapisan batas turbulen terjadi pada nilai kritis dari nomor Reynolds, Rexcr, sekitar 2 x 10^5 hingga 3 x 10^6, tergantung pada kasar permukaan dan jumlah turbulensi dalam aliran hulu, sebagaimana dibahas di Bagian 9.2.4. Seperti yang ditunjukkan oleh gambar di pinggiran, lokasi di sepanjang plat di mana aliran menjadi turbulen, xcr, bergerak menuju leading edge saat kecepatan aliran bebas meningkat.
Tujuan dari lapisan batas adalah memungkinkan fluida untuk mengubah kecepatannya dari nilai aliran di hulu, U, menjadi nol di permukaan. Dengan demikian, V =0 saat y =0 dan V ≈ Uˆi di tepi lapisan batas, dengan profil kecepatan, u yang bergantung pada x, y, membentuk ketebalan lapisan batas. Karakteristik lapisan batas ini terjadi dalam berbagai situasi aliran, tidak hanya pada plat datar. Sebagai contoh, lapisan batas terbentuk pada permukaan mobil, di air yang mengalir di saluran air di pinggir jalan, dan di atmosfer saat angin bertiup melintasi permukaan Bumi (daratan atau air).
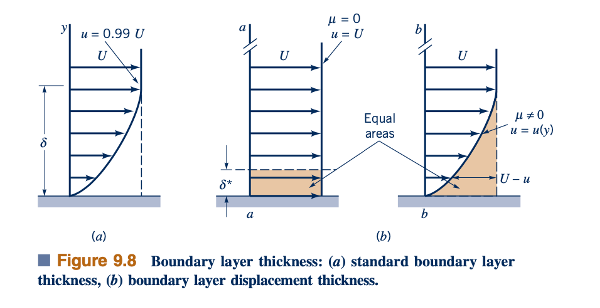
Sebenarnya (baik secara matematis maupun fisik), tidak ada "tepi" tajam pada lapisan batas; artinya, u menurun saat kita semakin jauh dari plat. Kami mendefinisikan ketebalan lapisan batas, δ, sebagai jarak dari plat di mana kecepatan fluida berada dalam beberapa nilai sembarang dari kecepatan di hulu. Biasanya, seperti yang ditunjukkan dalam Fig. 9.8a,
Untuk menghilangkan keragu-raguan ini (yaitu, apa yang istimewa dari 99%; mengapa bukan 98%?), definisi berikut diperkenalkan. Ditunjukkan dalam Gambar 9.8b adalah dua profil kecepatan untuk aliran di sekitar plat datar — satu jika tidak ada viskositas (profil seragam) dan yang lain jika ada viskositas dan tidak ada gesekan di dinding (profil lapisan batas). Karena defisit kecepatan, U ≤ u, dalam lapisan batas, debit aliran melintasi bagian b-b lebih kecil daripada yang melintasi bagian a-a. Namun, jika kita memindahkan plat di bagian a-a dengan jumlah yang sesuai 𝛿*, ketebalan perpindahan lapisan batas, debit aliran melintasi setiap bagian akan identik. Ini benar jika
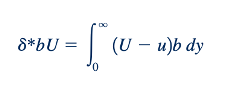
di mana b adalah lebar plat. Dengan demikian,
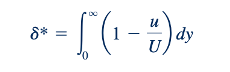
Ketebalan perpindahan mewakili jumlah peningkatan ketebalan tubuh yang diperlukan agar aliran imajiner tak berkepingan dan viskos tak berkepingan memiliki sifat laju aliran massa yang sama dengan aliran viskos aktual. Ini mewakili perpindahan keluar dari aliran garis yang disebabkan oleh efek viskos pada plat. Ide ini memungkinkan kita untuk mensimulasikan kehadiran lapisan batas pada aliran di luar lapisan batas dengan menambahkan ketebalan perpindahan ke dinding sebenarnya dan memperlakukan aliran di atas tubuh yang diperlebar sebagai aliran tak berkepingan. Konsep ketebalan perpindahan diilustrasikan dalam Contoh 9.3.

Definisi ketebalan momentum lapisan batas, 𝜃, sering digunakan saat menentukan gaya gesek pada suatu benda. Sekali lagi, karena defisit kecepatan, U - u, dalam lapisan batas, fluks momentum melintasi bagian b–b dalam Fig. 9.8 lebih kecil daripada fluks momentum melintasi bagian a–a. Defisit dalam fluks momentum untuk aliran lapisan batas aktual pada sebuah plat dengan lebar b diberikan oleh persamaan:
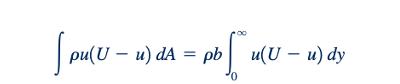
yang menurut definisi adalah fluks momentum dalam lapisan dengan kecepatan seragam U dan ketebalan 𝜃. Dengan demikian,

Atau

