Surface Normal Gradient

Gradien normal permukaan 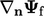$persamaan$ adalah bagian dari Persamaan diskritisasi Laplacian. (3.2), diilustrasikan pada gambar di bawah.

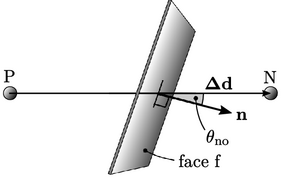
$GAMBAR\santai \khusus {t4ht=$

Diskritisasi 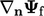$persamaan$ dibangun di atas perbedaan nilai sel yang terbatas pada setiap sisi permukaan sesuai dengan

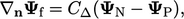rn f = C ( N P); \relax \special {t4ht=

(3.5)

Di mana 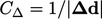$persamaan$ . Ketika skema ini ortogonal diterapkan pada Persamaan. (3.2) untuk mendiskritisasi Laplacian, ia membentuk koefisien 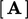$persamaan$ persamaan matriks 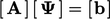$persamaan$ karena ia merujuk pada nilai sel bidang tersebut 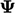$persamaan$ . 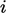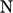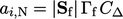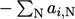Untuk sel $persamaan$ , koefisien setiap sel tetangga ( $persamaan$ ) adalah $persamaan$ dan koefisien diagonalnya adalah negatif dari jumlah koefisien tetangga: $persamaan$ .

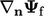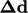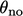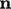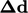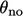Diskritisasi $persamaan$ oleh Persamaan. (3.5) paling akurat jika permukaannya ortogonalke $persamaan$ , yaitu sudut $persamaan$ antara $persamaan$ dan $persamaan$ adalah nol. Namun jika wajahnya tidak ortogonal , kesalahan yang terkait dengan Persamaan. (3.5) meningkat dengan $persamaan$ .

Koreksi non-ortogonal

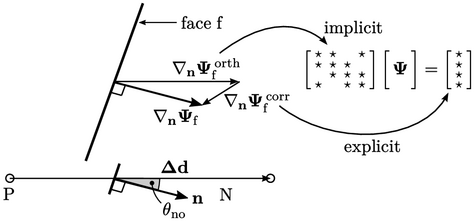
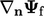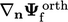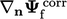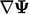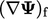Diskritisasi yang lebih akurat $persamaan$ pada permukaan non-ortogonal dibentuk dari jumlah vektor skema ortogonal $persamaan$ dan koreksi eksplisit $persamaan$ . Yang terakhir dihitung dari gradien penuh $persamaan$ di sel yang berdekatan (dijelaskan di Bagian. 3.15), disisipkan ke wajah $persamaan$ .

$GAMBAR\santai \khusus {t4ht=$

Koreksinya 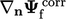$persamaan$ bersifat eksplisit, yaitu dihitung menggunakan nilai yang diketahui 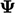$persamaan$ , sehingga mungkin perlu diperbarui dalam urutan berulang untuk menjaga akurasi, seperti yang dibahas di Bagian. 5.20. Untuk memastikan bahwa urutan iteratif menyatu, kontribusi implisitditingkatkan dengan mengganti $persamaan$ skema ortogonal dengan

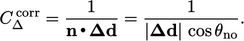corr ---1--- -----1------ C = n d = j dj cos no: \relax \special {t4ht=

(3.6)

Skema yang diperbaiki 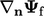$persamaan$ menggabungkan bagian implisit dan eksplisit dengan

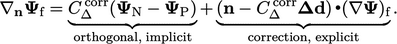r = C corr( )+ (n C corr d) (r ) : n f |--------------------{Nz--------------P------} |-----------------------------{z-----------------------------}f orthogonal, implicit correction, explicit \relax \special {t4ht=

(3.7)

Skema yang dikoreksi umumnya stabil untuk 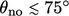$persamaan$ . Sebab 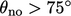$persamaan$ , stabilitas dapat dipertahankan dengan mengorbankan keakuratan dengan membatasi besarnya koreksi 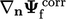$persamaan$ di bawah sebagian kecil dari besarnya 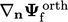$persamaan$ bagian ortogonal.