5.2 The Semi-Discretized Equation
In langkah 1 dari proses diskritisasi volume terhingga, persamaan yang mengatur diintegrasikan melalui elemen (atau volume terhingga) ke dalam domain yang telah dibagi-bagi, kemudian teorema Gauss diterapkan untuk mentransformasikan integral volume dari istilah adveksi dan difusi menjadi integral permukaan. Setelah langkah ini, integral permukaan dan volume ditransformasikan menjadi integral diskrit dan diintegrasikan secara numerik melalui penggunaan titik integrasi (ip). Untuk menjelaskan pendekatan ini dan untuk mengembangkan penghargaan yang memadai terhadap subtilitas skema diskritisasi lanjutan yang dibahas dalam bagian-bagian berikutnya, contoh berikut mengilustrasikan aplikasi teknik tersebut untuk masalah transportasi dua dimensi. Seperti yang disajikan dalam Bab 3, persamaan konservasi untuk variabel skalar umum
Berdasarkan yang disajikan dalam Bab 3, persamaan konservasi untuk variabel skalar umum dapat diekspresikan sebagai:
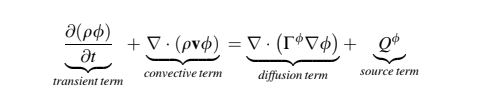
Bentuk keadaan tetap dari persamaan di atas diperoleh dengan mengabaikan istilah transien dan diberikan oleh.
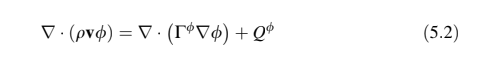
Dengan mengintegrasikan persamaan di atas melalui elemen C yang ditunjukkan dalam Gambar 5.1, Persamaan (5.2) ditransformasikan menjadi.
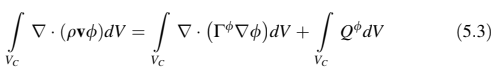
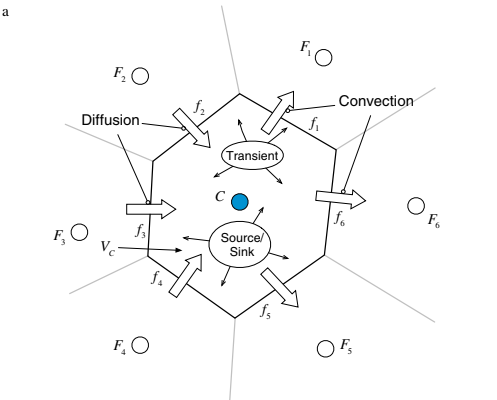
Dengan mengganti integral volume dari istilah adveksi dan difusi dengan integral permukaan melalui penggunaan teorema divergensi, persamaan di atas menjadi.
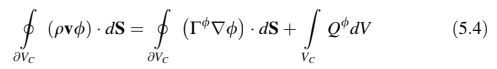
di mana huruf tebal menunjukkan vektor, (·) adalah operator perkalian titik, merupakan istilah sumber, S vektor permukaan, v vektor kecepatan, / kuantitas yang dilestarikan,
dan integral permukaan atas volume
Baca juga: Boundary Conditions
