Spesifik Dissipasi Rate

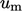Model ini merupakan salah satu dari keluarga model dua persamaan untuk turbulensi. Dengan dua persamaan, model dapat mewakili masing-masing skala, dan 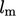, yang mencirikan 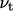. Paling sering, 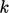digunakan untuk mewakili .

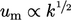Variabel lainnya harus mewakili 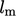dan selama ini kita gunakan 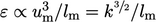dengan satuan SI 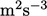. Laju disipasi spesifik 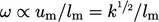, dengan satuan SI 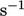, merupakan alternatif populer untuk variabel ini dalam pemodelan turbulensi.

Meskipun Kolmogorov pertama kali mengusulkan model dua persamaan ,¹⁵ model yang digunakan dalam CFD berasal dari Wilcox.¹⁶ Di sini yang dimaksud dengan “model” adalah jamak karena terdapat beberapa versi model yang mengalami modifikasi dan penambahan dari bentuk aslinya.

Model aslinya _disajikan di bawah ini (dengan beberapa perubahan pada nama variabel asli), dengan asumsi 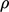= konstan untuk perbandingan langsung dengan di Sec. 7.1.

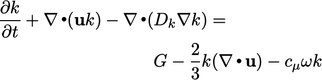$@k-+ r (uk) r (D rk) = @tk 2- G 3 k(ru) c !k \relax \special {t4ht=$

(7.36)

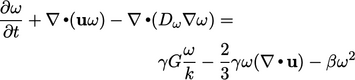$@!- @t + r (kamu!) r (D!r!) = ! 2 G-- - -!(ru) !2 k 3 \santai \khusus {t4ht=$

(7.37)

Koefisien model standarnya adalah

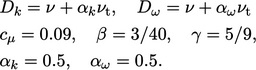$Dk = +kt; D! = + ! tc = 0.09; = 3=40; = 5=9; = 0:5; = 0:5: k ! \santai \khusus {t4ht=$

(7.38)

Membandingkan istilah disipasi dalam Persamaan. (7.1) dan Persamaan. (7.36) memberikan hubungannya 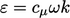. Mengganti dalam Persamaan. (6.31) menghasilkan hubungan sederhana untuk viskositas turbulen, yang diberikan oleh

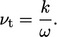$k- t = ! : \relax \special {t4ht=$

(7.39)

Perkiraan masuk dan awal untuk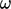dapat dihitung dengan

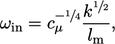$1 k1=2 !in = c =4---; lm \relax \special {t4ht=$

(7.40)

menggunakan 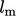, dengan cara yang mirip dengan 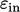Persamaan. (7.4).

Dengan fungsi dinding, kondisi batas diterapkan untuk 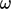menetapkan nilai sel dekat dinding menurut

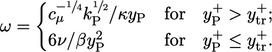$(c 1=4k1=2= yP for y+ > y+; ! = P2 P+ tr+ 6 = yP for yP ytr: \relax \special {t4ht=” style=”vertical-align: bottom; margin-bottom: 0px;”></center></td> <td style=$ (7.41)

Ekspresi untuk 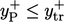( 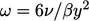) adalah solusi persamaan berikut untuk sublapisan kental dimana suku difusi dan disipasi mendominasi pada Persamaan. (7.37):

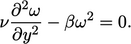$2 @-!- !2 = 0: @y2 \relax \special {t4ht=$ (7.42)

Istilah disipasi yang setara 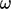dalam Persamaan. (7.37) dan 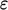dalam Persamaan. (7.2) adalah 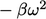dan 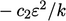masing-masing. Yang pertama lebih stabil dalam solusi numerik karena tidak peka terhadap variasi .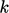