Under relaxation

Detik. 5.5 menyimpulkan bahwa matriks persamaan transpor tipikal tidak dijamin dominan secara diagonal. Oleh karena itu, beberapa tindakan mungkin diperlukan untuk memastikan solusi yang konvergen.

Relaksasi bawah adalah metode umum yang digunakan untuk meningkatkan konvergensi solusi dengan membatasi jumlah perubahan variabel selama langkah solusi.

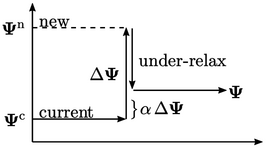
$GAMBAR\santai \khusus {t4ht=$

Selama langkah solusi, asumsikan nilai tunggal bidang 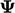$persamaan$ dalam satu sel berubah dari nilai saat ini 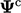$persamaan$ ke nilai baru 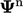$persamaan$ . Relaksasi yang kurang akan membatasi perubahan 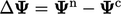$persamaan$ sebesar pecahan 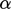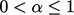$persamaan$ ,, $persamaan$ sehingga nilai yang diambil dari langkah penyelesaian tersebut adalah

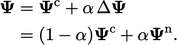= c + c n = (1 ) + : \relax \special {t4ht=

(5.13)

Dalam beberapa situasi, Persamaan. (5.13) diterapkan setelah langkah solusi. Pendekatan sederhana ini dikenal dengan istilah field under-relaxation, yang memiliki satu kelemahan penting yaitu memerlukan penyimpanan tambahan pada bidang perantara 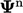$persamaan$ di memori komputer.

Ketika langkah solusi melibatkan penyelesaian persamaan matriks, nilai baru 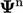$persamaan$ berasal dari metode berulang seperti Gauss-Seidel. Menggabungkan relaksasi yang kurang dari Persamaan. (5.13) dengan perhitungan Gauss-Seidel dari Persamaan. (5.4) memberi:

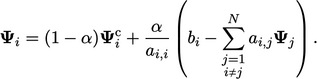0 1 c ---BB XN CC i = (1 ) i + ai;i@bi ai;j jA : ji=⇔1j \relax \special {t4ht=

(5.14)

Menata ulang Persamaan. (5.14) memberikan hubungan berikut:

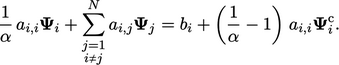XN 1-ai;i i + ai;j j = bi + 1- 1 ai;i ci: j=1 i⇔j \relax \special {t4ht=

(5.15)

Persamaan 5.15 hanyalah persamaan matriks 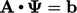$persamaan$ yang dimodifikasi oleh:

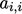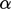meningkatkan koefisien diagonal $persamaan$ dengan membaginya $persamaan$ ;
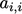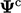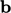mengalikan selisih antara $persamaan$ koefisien baru dan asli dengan arus $persamaan$ dan menambahkannya ke sumber $persamaan$ .

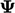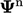Memodifikasi persamaan matriks dengan cara ini disebut persamaan relaksasi bawah, memberikan alternatif untuk Persamaan. (5.13) untuk solusi yang kurang menenangkan $persamaan$ , tanpa penyimpanan sementara $persamaan$ .

Memastikan dominasi diagonal

Modifikasi yang 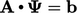$persamaan$ diungkapkan oleh Persamaan. (5.15) menginspirasi strategi untuk memastikan dominasi diagonal matriks sebagai berikut.

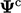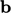Setiap koefisien diagonal yang tidak memenuhi Persamaan. (5.9) diperbesar hingga diagonalnya sama. Perubahan koefisien dikalikan dengan arus $persamaan$ dan ditambahkan ke $persamaan$ .

Pendekatan untuk memastikan dominasi diagonal ini efektif karena hanya mengubah koefisien matriks jika diperlukan. Sebaliknya, jika skema diskritisasi 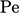$persamaan$ menguntungkan 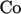$persamaan$ , maka tidak diperlukan perubahan pada matriks.